Предмет: Геометрия,
автор: хомяк04
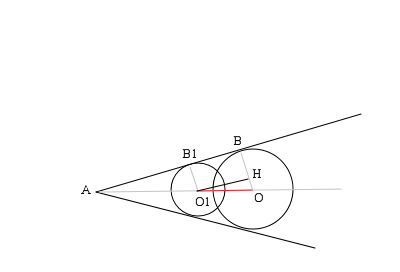
ПОМОГИТЕ С РИСУНКОМ!!!!Две окружности с центрами в точках О и О1 и радиусами 5 и 3 соответственно касаются сторон угла А (В и В1 – точки касания). Найдите расстояние между центрами окружностей, если АВ1=4.
Ответы
Автор ответа:
0
центры окружностей будут лежать на биссектрисе угла А
радиусы окружностей (О1В1 и ОВ), проведенные в точки касания _|_ строне угла
получившаяся фигура ОВВ1О1 ---прямоугольная трапеция
проведем О1Н || В1В
получившиеся треугольники АВ1О1 и О1НО подобны (по двум углам: они прямоугольные, углы В1АО1=НО1О равны)
НO / В1O1 = О1О / АО1
О1О = АО1 * НO / В1O1
по т.Пифагора (АО1)^2 = (AB1)^2 + (B1O1)^2 = 4^2 + 3^2 = 16+9 = 25
AO1 = 5
HO = 5-3 = 2 (по построению НВВ1О1 ---прямоугольник)
O1O = 5*2/3 = 10/3 = 3целых 1/3
Приложения:
Похожие вопросы
Предмет: Химия,
автор: katyababenko05
Предмет: История,
автор: ermakovanina16
Предмет: Русский язык,
автор: annaasenina702
Предмет: Математика,
автор: савав