Предмет: Геометрия,
автор: tanya69
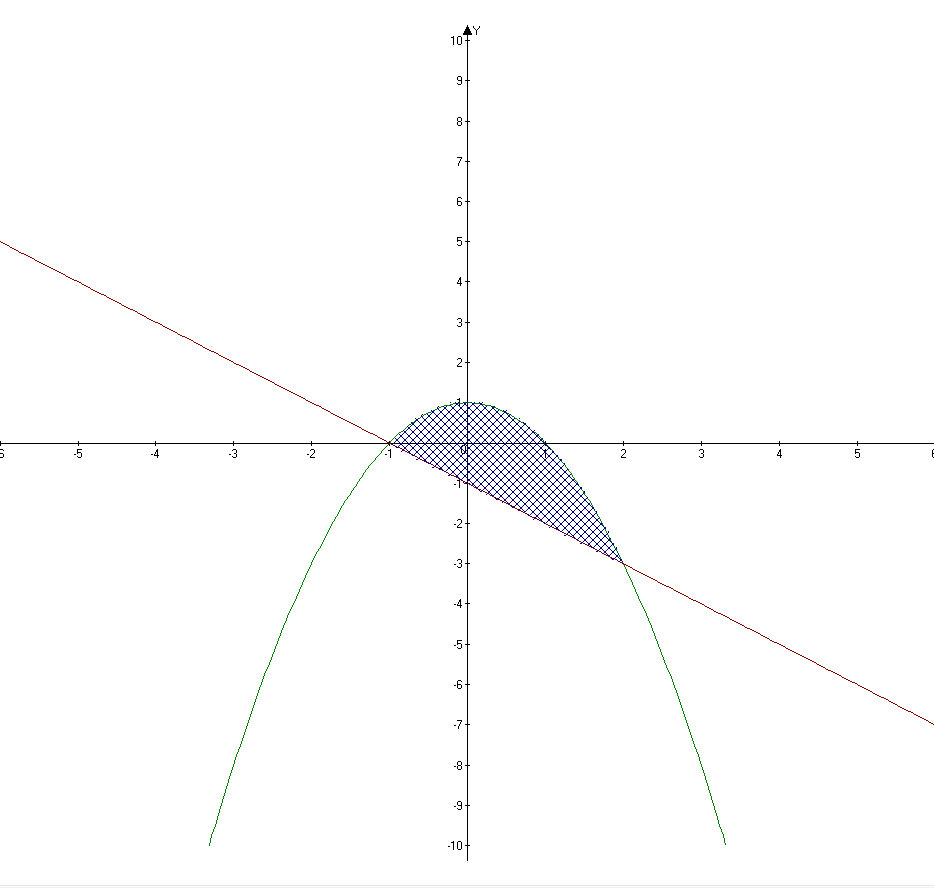
вычислите площадь фигуры, ограниченной графиками функций: y=1-x^2, y=-x-1.
Ответы
Автор ответа:
0
Sfig=
Вот график и область фигуры:
Приложения:
Автор ответа:
0
Парабола пересекается с прямой в точках -1 и 2. Она находится выше прямой, значит вычитаем из неё прямую
S =
Приложения:

Похожие вопросы
Предмет: История,
автор: cmhauck33
Предмет: Математика,
автор: dariarad09
Предмет: Українська мова,
автор: glushko82
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: 1sparrow