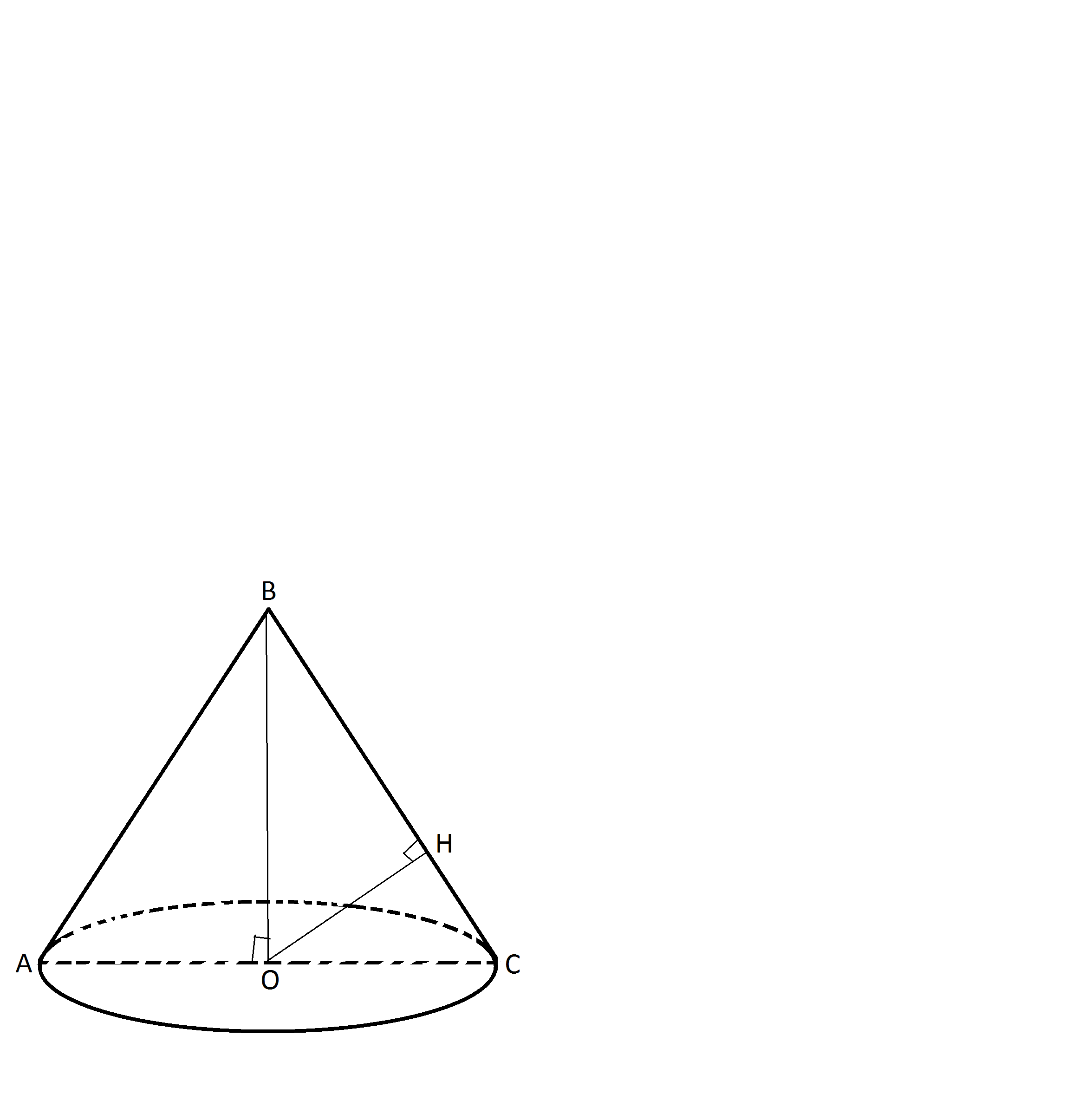
высота конуса равна 20 см, расстояние от центра до образующей равна 12 см.Найдите площадь поверхности конуса
Ответы
высота=20
перпендикуляр из центра основания к образующей=12
получаем два подобных прямоугольных треугольника
20/16=х/12
х=15
образующая=25 (20*20+15*15=625)
радиус=15
Боковая поверхность=πrl=π*15*25=375π
Площадь основания=πr²=π*15²=225π
Полная поверхность=375π+225π=600π
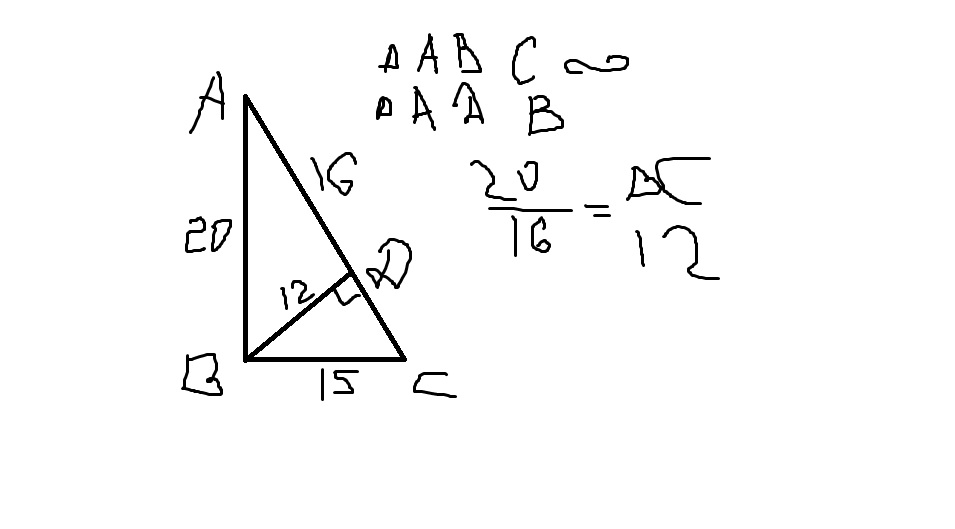
Площадь поверхности конуса = площадь основания + площадь боковой поверхности:
S =πr²+πrL=πr(r+L)
Радиус и образующую нaйдем из прямоугольного треугольника ВОС,
где ВО - высота конуса,
ВС - образующая,
ОН - расстояние от центра основания конуса до образующей и в то же время
высота треугольника ОВС.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
.
Из прямоугольного треугольника ВОН найдем по т.Пифгора отрезок ВН.
Треугольник - египетский с отношением сторон 3:4:5, можно обойтись и без Пифагора - коэффициент отношения сторон 20:5=4, и
ВН=14*4= 6.
( но и т.Пифагора всегда будет в помощь)
ОН²=ВН*СН
144==16 СН
СН=9
Из треугольника СНО ( и он египетский)
ОC =15.
ОC=R
L=BC=16+9=25
S =πr(r+L)=π15(15+25)=600π