Question

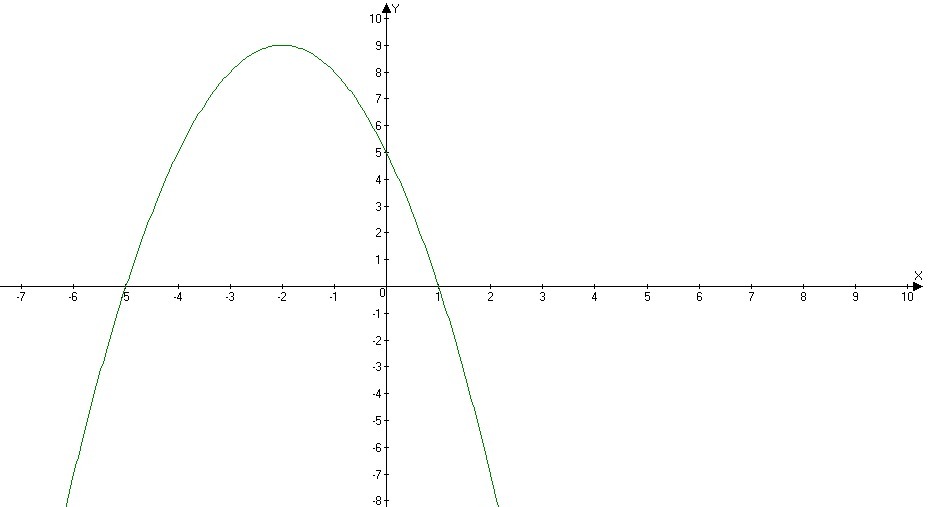
дана функция y=-x²-4x+5 Какие утверждения являются верными
1) x=-5, y=0
2) функция убывает в промежутке (-бесконечности; -2]
3) у>0 при -5<х<1
4) у=0, х=3

Answer 1

1) Если $x=-5$, то значение функции в этой точке
$y=-(-5)^2-4cdot(-5)+5=-25+20+5=0$

Поэтому, первый вариант будет верным.

2) Найдем координаты вершины параболы:
$m=- dfrac{b}{2a} =- dfrac{-4}{2cdot(-1)} =-2$ координата X
$y(-2)=-(-2)^2-4cdot(-2)+5=-4+8+5=9$
$(-2;9)$ -координаты вершины параболы.
Графиком функции является парабола, ветви направлены вниз, значит эта функция убывает на промежутке $(-2;+infty)$

3) $y textgreater 0$, то есть $-x^2-4x+5 textgreater 0|$
По графику видим, при у>0 будет промежуток $-5 textless x textless 1$

Да, это верно.

4) Если $y=0$, то $0=-x^2-4x+5$ и это квадратное уравнение с корнями x1 = -5; x2 = 1

Нет, не верно