Question

дослідити функцію f(x)=x^3 - 4x на монотонність та екстермуми

Answer 1

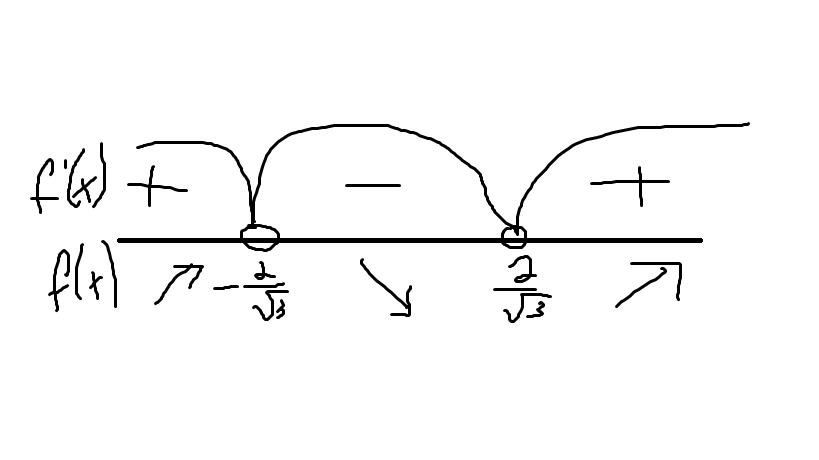
Найдём производную функции, приравняем к нулю, чтобы найти критические(стационарные) точки.

$f'(x)=(x^3-4x)'=3x^2-4\f'(x)=0\3x^2-4=0\x^2=frac{4}{3}\x=бfrac{2}{sqrt{3}}$

Вложение.

Монотонность: $(-infty;-frac{2}{sqrt{3}}]$ - возрастает.

                             $(-frac{2}{sqrt{3}};frac{2}{sqrt{3}}]$ - убывает.

                             $(frac{2}{sqrt{3}};+infty)$ - возрастает. 

Экстрэмумы: $-frac{2}{sqrt{3}}$ - точка максимума функции. 

                          $frac{2}{sqrt{3}}$ - точка минимума функции.