Предмет: Алгебра,
автор: 4ukistov
Решите неравенство
sqrt(2x^2-18x+16)+4<x
Приложения:
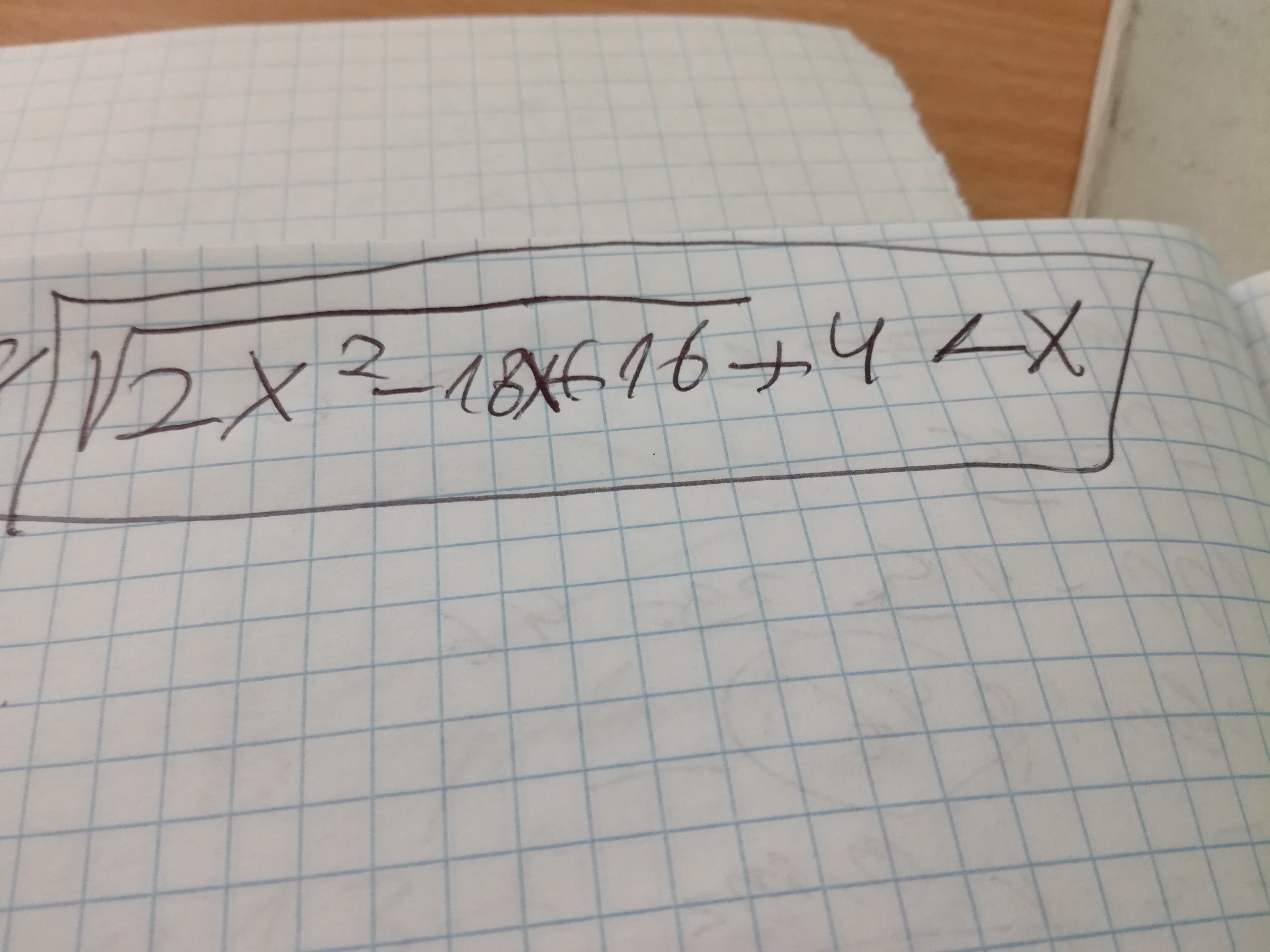
Ответы
Автор ответа:
0
решаем первое неравенство
нули функции х-1=0, х=1
х-8=0, х=8
коэффициент при x^2 равен 1(ветви параболы верх), значит решение
х є
решаем второе
нули функции х=0,
х-10=0, х=10
коэффициент при x^2 равен 1 (ветви параболы верх) ,значит решение
х є (0;10)
обьдиняя находим решение
x є
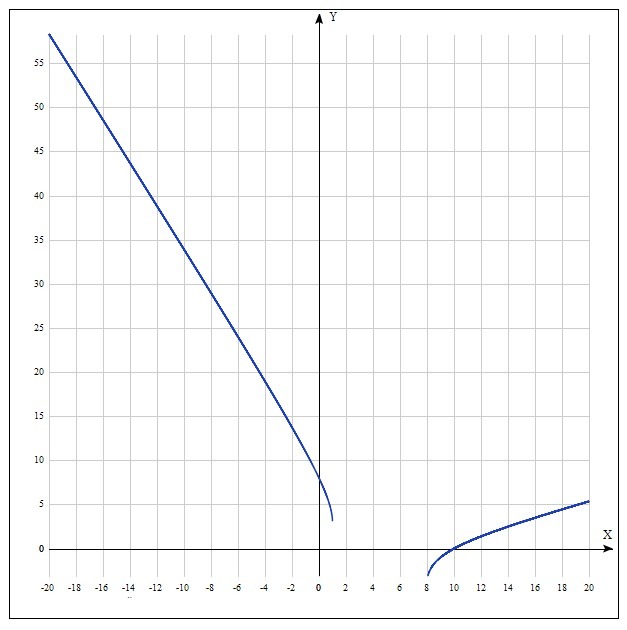
во вложении граффик
по граффику видно что л.ч. отрицательная при x є
Приложения:

Автор ответа:
0
почему при постановке единицы вместо x получается 4<0? Значит решение неправильное?
Похожие вопросы
Предмет: Физика,
автор: lukomskaaketrin
Предмет: Українська мова,
автор: romankovalcuk162
Предмет: Химия,
автор: komteh17032016
Предмет: Биология,
автор: Nika0925
Предмет: Биология,
автор: ИнгушкаИнгушева