Доказать тождество (1+cos(a/2) - sin(a/2))/(1-cos(a/2)-sin(a/2)) = -ctg(a/4)
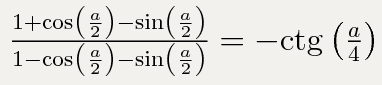
Ответы
представляем соs и sin как двойные углы
(1+сos^2 a/4 -sin^2 a/4 -2sin a/4 cos a/4)/(1-cos^2 a/4 + sin^2 a/4 -2 sin a/4 cos a/4)= -ctg a/4
группируем: 1-sin^2 a/4=cos^2 a/4 в числителе
1-соs^2 a/4=sin^2 a/4 в знаменателе
(cos^2 a/4+cos^2 a/4 -2sin a/4 cos a/4)/(sin^2 a/4+sin^2 a/4 - 2 sin a/4 cos a/4)= -ctg a/4
(2cos^2 а/4-2sin a/4 cos a/4)/(2sin^2 a/4 -2 sin a/4 cos a/4)= -ctg a/4
2cos a/4(cos a/4- sin a/4)/-2 sin a/4(cos a/4-sin a/4)= -ctg a/4
cos a/4 /-sin a/4=-ctg a/4
- ctg a/4=-ctg a/4 (верно)
Тождество верно
докажем вот так
-ctg(a/4)=-ctg(a/2/2)=-1-cos(a/2)/sin(a/2)
(1-sina+cosa)(1-sina-cosa)/(1-cosa-sina)^2
((1-sina)^2-cos^2a)/(1-cosa-sina)^2
((1-2sina+sin^2a-cos^2a)/((1 + sin^2 a + cos^2 a - 2sin a - 2cos a + 2sina*cosa) =
(2sin^2a-2sina)/(2-2sina-2cosa+2sinacosa)= sin^2a-sina/(1-sina-cosa+sinacosa) =
sina(sina-1) / (-sina+1 - cosa(1-sina)
-sina+1 = -(sina-1)
-cosa+sinacosa=cosa (sina-1)
-(sina-1)+cosa(sina-1)= (cosa-1)(sina-1)
ставим
sina/cosa-1
что и требовалось доказать