Предмет: Геометрия,
автор: илья20122002
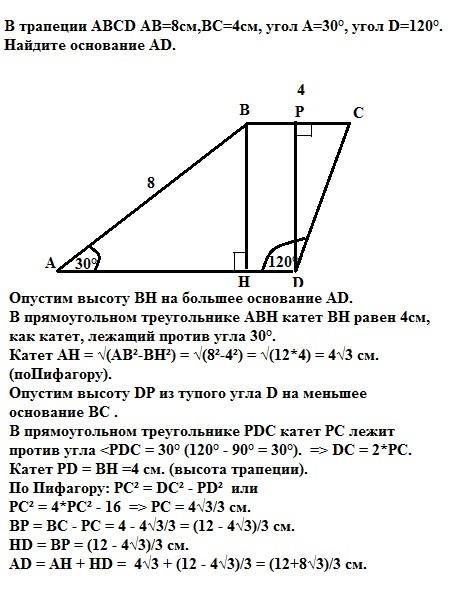
В трапеции ABCD AB=8см,BC=4см, угол А=30*,угол D=120*.Найдите основание AD
Ответы
Автор ответа:
0
Ответ:
AD = (12+8√3)/3 см.
Объяснение:
Опустим высоту ВН на большее основание AD.
В прямоугольном треугольнике АВН катет ВН равен 4см, как катет, лежащий против угла 30°.
Катет АН = √(АВ²-ВН²) = √(8²-4²) = √(12*4) = 4√3 см. (по Пифагору).
Опустим высоту DP из тупого угла D на меньшее основание ВС .
В прямоугольном треугольнике PDC катет PС лежит против угла
PDC = 30° (120° - 90° = 30°). => DC = 2*PC. Катет
PD = ВН =4 см. (высота трапеции).
По Пифагору: РС² = DC² - PD² или
РС² = 4*РС² - 16 => РС = 4√3/3 см.
ВР = ВС - РС = 4 - 4√3/3 = (12 - 4√3)/3 см.
HD = BP = (12 - 4√3)/3 см.
AD = AH + HD = 4√3 + (12 - 4√3)/3 = (12+8√3)/3 см.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: ppptttt
Предмет: Математика,
автор: shushkovazhanna
Предмет: Українська мова,
автор: tanaskrut
Предмет: Математика,
автор: Аррианночка
Предмет: Математика,
автор: leraddytf