Question

1)Основание равнобедренного треугольника равно 16 см, а боковая сторона 17 см. Найдите площадь треугольника

2)ромба относятся как 4 : 5, а его площадь равна 40 см2. Найдите диагонали ромба

Answer 1

1) Проведем высоту из вершины равнобедренного треугольника, по его свойствам она будет медианой, следовательно разделит основания на равные отрезки по 8. В прямоугольном трегольники ABH, по теореме Пифагора следует BH^2=AB^2-AH^2

BH^2=289-64; BH=15, 

S=AC*BH/2

S=15*16/2=120 см^2

2) Диагонали ромба относятся как 4 : 5, а его площадь равна 40 см2. Найдите диагонали ромба. Наверное так..?

d1/d2=4/5, 4d1=5d2, d1=5d2/4, d1=1,25d2

Пусть первая диагональ это x, тогда вторая 1.25x, подставим в формулу площади ромба S=d1*d2/2 

S=x*1.25x/2, 40=1.25x^2/2, решив уравнение получим x=8, значит вторая диагональ равна d2=1.25* 8=10

Ответ: 8 см и 10 см

 

Answer 2

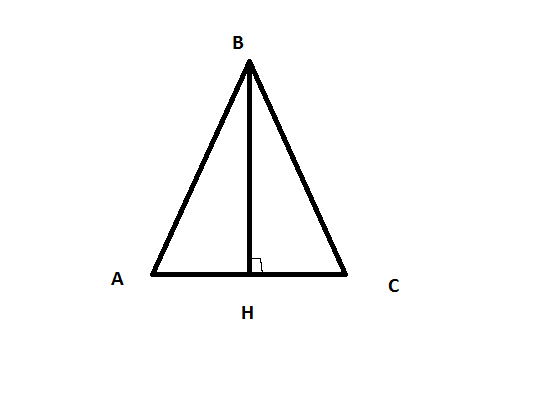
1)

Найдем величину высоты данного треугольника:

$h=sqrt{17^2-8^2}=15$

Тогда площдь будет равна:

$S=fac12ah=frac12*16*15=8*15=120$ где h- высота проведенная к стороне а.

Ответ: 120

2)

Так как диагонали ромба относятся в отношении 4:5, а площадь ромба равна:

$S=frac{d_1d_2}{2}$

Откуда получаем:

$d_1d_2=2S=80$

Известно, что;

$frac{d_1}{d_2}=frac45$

Получаем:

$d_1=frac45d_2$

Тогда:

$d_1d_2=80$

$frac45d_2^2=80$

$d_2^2=100$

$d_2=10$

Тогда:

$d_1=frac45*10=8$

Ответ: 8 и 10