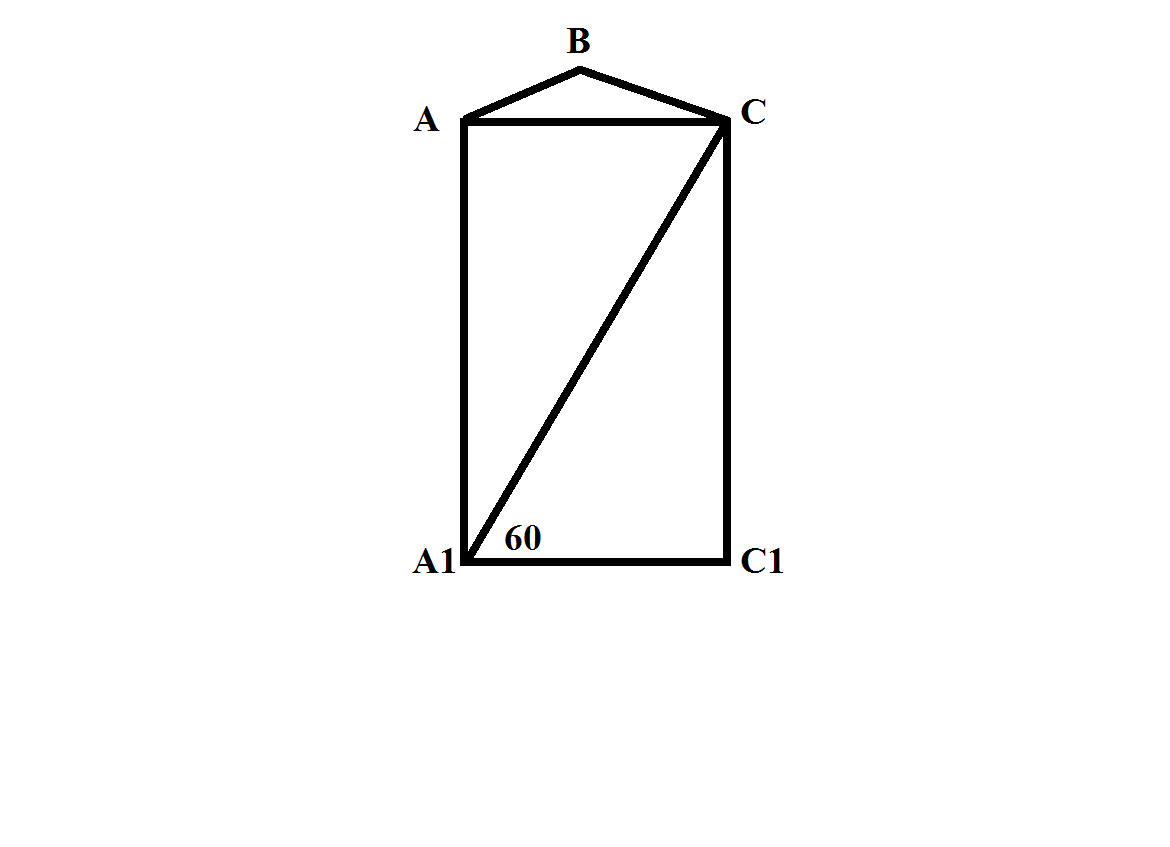
1. в основании прямой треугольной призмы лежит прямоугольный треугольник с катетами 3 и 4см. Диагонали большой боковой грани наклонены к плоскости основания под углом 60 градусов. Найти S полн. призмы
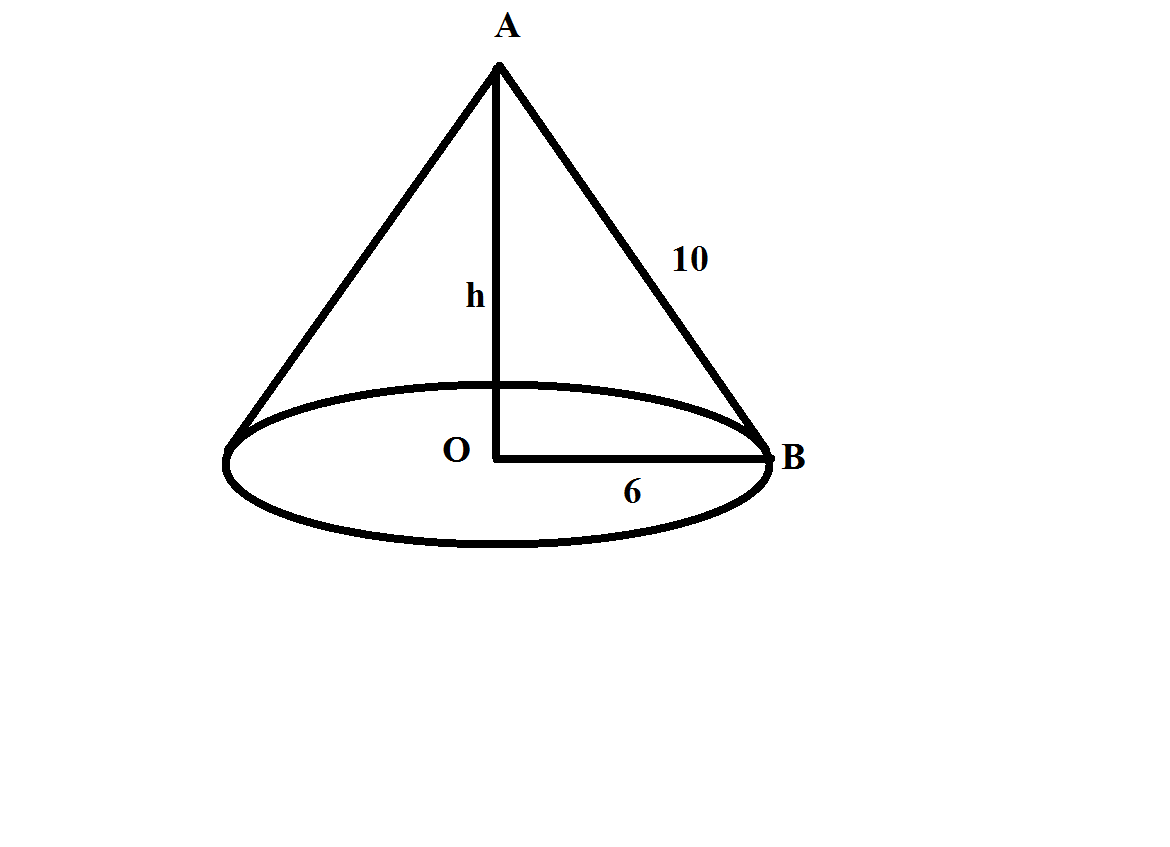
2. Образующая конуса равна 10 см, а радиус основания 6. Найти объем конуса.
Если можно с пояснениями.
Ответы
№1
S полн. призмы=2S основ.+S бок.
В основании призмы - прямоуг. треугольник
SΔ=½ah
2S основ=2SΔ=3*4=12(см²)
S бок=РΔ*h
Найдем в треугольнике гипотенузу по теор. Пифагора
АС=√АВ²+ВС²=√3²+4²=√25=5 (см)
Найдем высоту призмы CC₁
Δ А₁СС₁ - прямоугольный
СС₁/А₁С₁=tq 60°
CC₁=A₁C₁ * tq 60°
tq 60°=1,73
СС₁=5*1,73≈8,65(см)
S бок=РΔ*h
S бок=(3+4+5)*8,65
S бок=103,8(см²)
S полн. призмы=2S основ.+S бок.
S полн. призмы=12+103,8
S полн. призмы =115,8(см³)
№2
АО=h - высота конуса
АВ= 10cм - образующая конуса
ОВ=6см - R основания
V - ?см³
V=⅓πR²h
найдем высоту конуса АО
Δ АОВ - прямоугольный
ОВ, ОА - катеты
АВ - гипотенуза
АО=√ АВ² - ОВ²
АО=√10²-6²=√64=8(см)
V=3,14*6²*8:3
V конуса ≈301,44(см³)