Question

Основание пирамиды ДАВС является треугольник со сторонами АС=АВ=15 см,СВ=18 см. боковое ребро да перпедикулярно плоскости основания и равно 9 см. Найдите площадь полной поверхности пирамиды

Answer 1

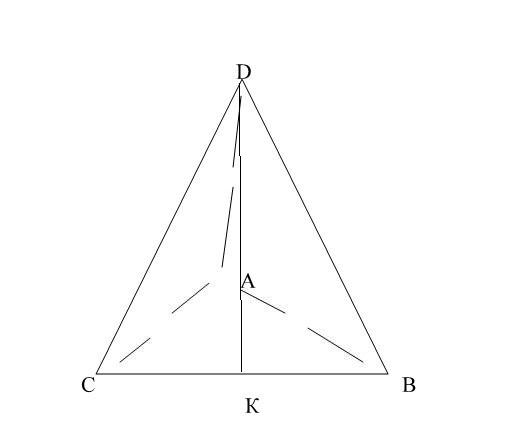
Дана треугольная пирамида ABCD, в основании которой равнобедренный треугольник ABC (АС=АВ=15, ВС=18).

 

DA перпенддикулярно плоскости АВС.

Рассмотрим треугольник DAB-прямоугольный.

DB^2 = DA^2 + AB^2

DB = корень из 306

DC=DB

 

Проведем перпендикуляр DK в треугольнике CDB.Треугольник CDB-равнобедренный.

СК=КВ=9

Рассмотрим треугольник CKD-прямоугольный.

DK^2 = CD^2 - CK^2

DK=15

 

Sп.п. = S(CAD) + S(BAD) + S(CDB)

S(CAD) = (DA*AC)/ 2 = (9*15)/2 = 67,5

S(BAD) = S(CAD) = 67,5

S(CDB) = (DK*BC) / 2 = (15*18)/2= 135

 

Sп.п. = 67,5 + 67,5 + 135=270.