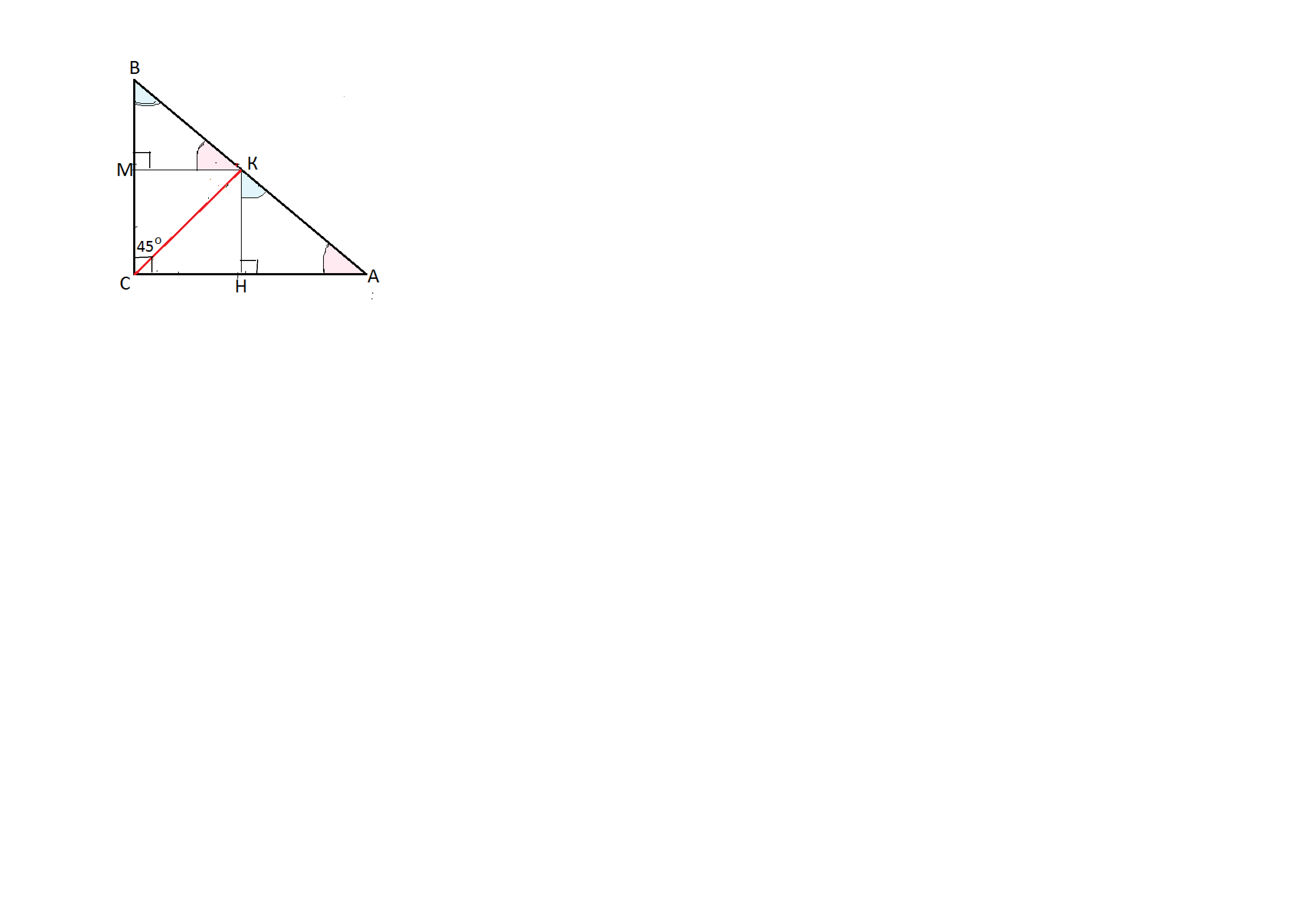ПОМОГИТЕ ПОЖАЛУЙСТА!
Из вершины прямого угла прямоугольного треугольника проведена биссектриса, которая делит гипотенузу на части 30см и 40см. Найдите расстояние от точки деления до катетов.
Ответы
Дано:∆ АВС - прямоугольный, угол С =90º
СК - бисскетриса.
ВК=30
АК=40
Решение задачи начнем с рисунка.
Биссектриса внутреннего угла треугольника делит сторону на отрезки, пропорциональные прилежащим сторонам.
Это относится ко всем треугольникам.
Из этого отношения следует отношение катетов:
ВС:АС=30:40=3:4
Пусть коэффициент отношения катетов будет х.
Тогда
ВС=3х
АС=4х
По т.Пифагора
АВ²=ВС²+АС²
70²=9х²+16х²=25х²
х²=196
х=14
АС=4*14=56 с
ВС=3*14=42 см
Опустим из точки К перпендикуляр КН на АС ( расстояние от точки до прямой -перпендикуляр)
КН║ВС, ∠ А общий
∆ АКН подобен ∆АВС
Из подобия
АВ:АК=ВС:КН
70:40=42:КН
КН=1680:70=24 см
Тем же способом из подобия КМВ и АВС найдем МК=24 (можно проверить).
Но треугольники ВМК и АНК не равны, как может показаться.
В них равные катеты лежат против разных углов.
АН=56-24=32 см
ВМ=42-24=18 см
Найдя КН, можно не находить отдельно расстояние КМ.
МКНС - квадрат, т.к. ∠С=90º по условию, ∠КАМ=∠КНС=90º по построению, а диагональ -биссектриса угла С
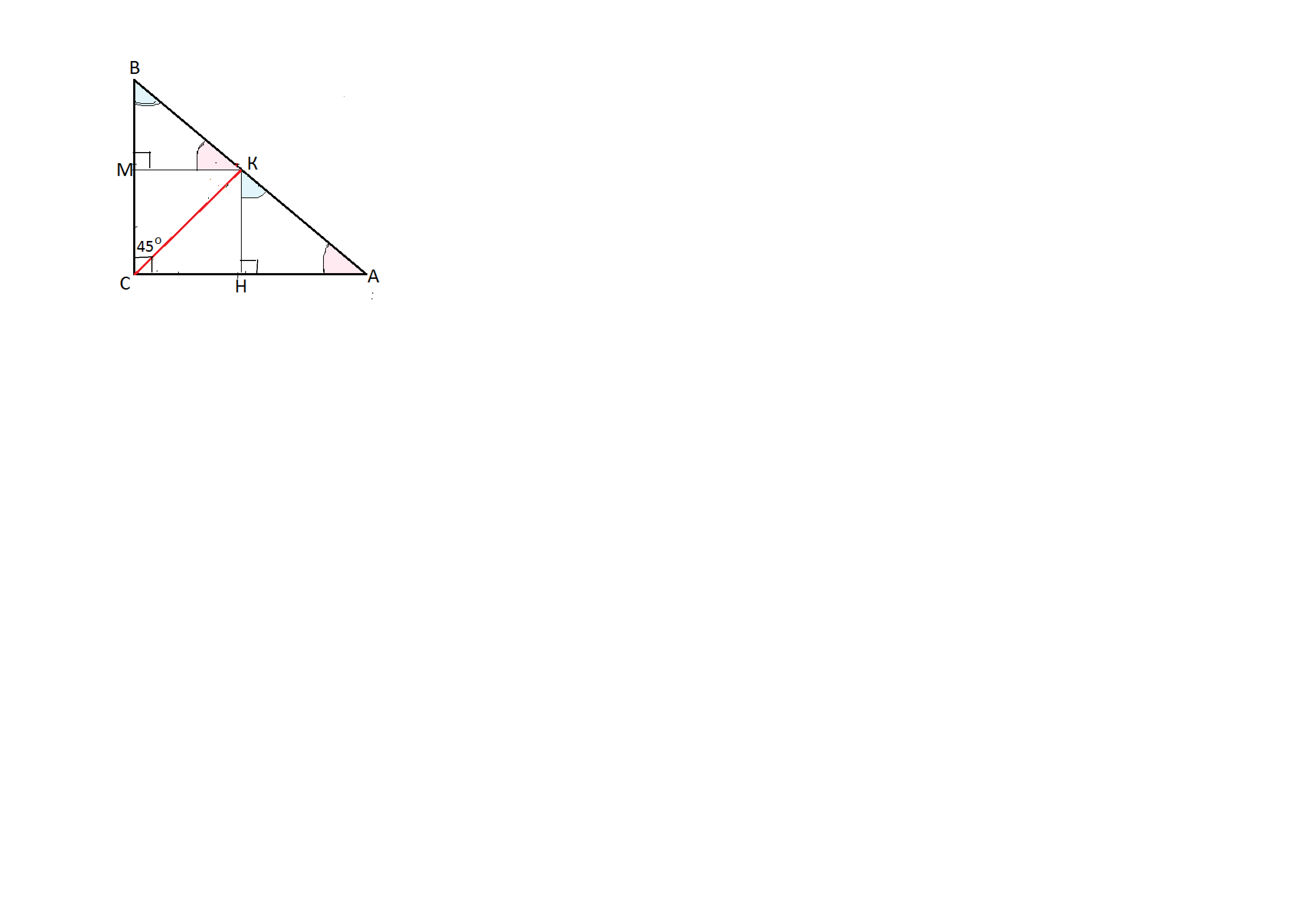
Точка, лежащая на биссектрисе угла равно удалена от сторон угла. Значит, расстояние от точки деления до катетов одинаковое. Примем его за х. Тогда из подобия двух прямоугольных треугольников с вершинами в точках А и В С=90, получаем
30:40 = х:у, где у - расстояние от перпендикуляра на основание до точки В. у=4х/3. Из теоремы Пифагора имеем
40^2 = x^2 + (4x/3)^2 x^2 +16x^2/9 = 1600 25x^2/9 = 1600 x^2 = 1600*9/25 x=24.
Расстояние от точки деления до катетов 24 см.