Предмет: Математика,
автор: catty20011
30 баллов за решение!
Приложения:
Ответы
Автор ответа:
0
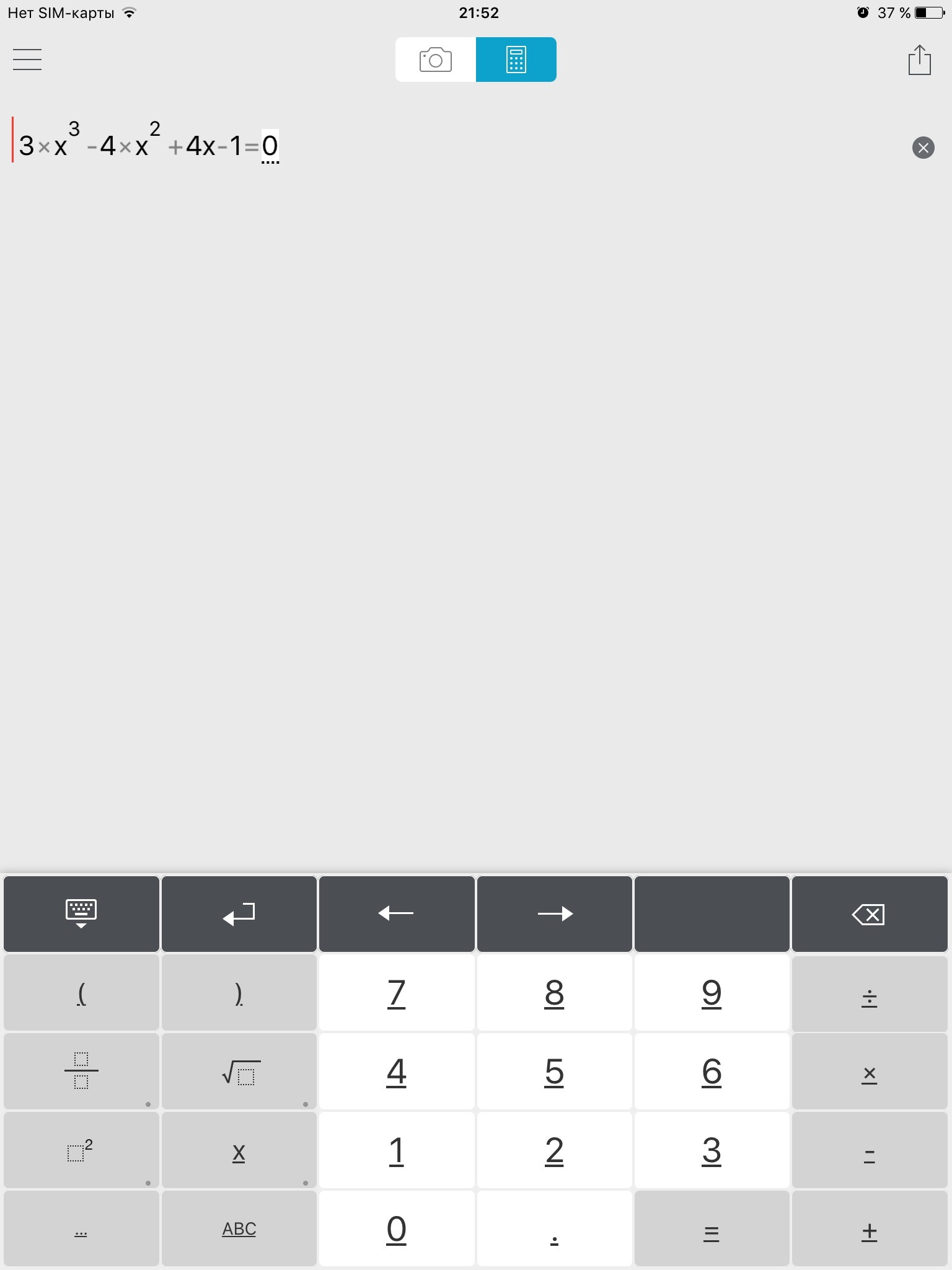
3x^3 - 4x^2 + 4x - 1 = 0
Обычное кубическое уравнение.
Решаем методом Кардано. Жаль, что его в школе не проходят.
1) Замена x = y + 4/9. Цель - избавиться от члена x^2
3(y+4/9)^3 - 4*(y+4/9)^2 + 4(y+4/9) - 1 = 0
3(y^3+3*4/9*y^2+3*(4/9)^2*y+(4/9)^3)-4(y^2+2*4/9*y+(4/9)^2)+4y+16/9-1=0
3y^3+4y^2+16/9*y+64/243-4y^2-32/9*y-64/81+4y+16/9-1 = 0
3y^3 + (16/9-32/9+36/9)*y + (64/243-64/81+7/9) = 0
Делим на 3
y^3 + 20/27*y + (64-192+7*27)/243 = 0
y^3 + 20/27*y + 61/729 = 0
Классическое кубическое уравнение вида
y^3 + py + q = 0; где p = 20/27 = 20/3^3; q = 61/729 = 61/3^6
Дискриминант


Корень
![y= sqrt[3]{- frac{q}{2}- sqrt{Q}}+sqrt[3]{- frac{q}{2}+ sqrt{Q}}=sqrt[3]{- frac{61}{2*3^6}- frac{189}{2*3^6} }+sqrt[3]{- frac{61}{2*3^6}+frac{189}{2*3^6} }= y= sqrt[3]{- frac{q}{2}- sqrt{Q}}+sqrt[3]{- frac{q}{2}+ sqrt{Q}}=sqrt[3]{- frac{61}{2*3^6}- frac{189}{2*3^6} }+sqrt[3]{- frac{61}{2*3^6}+frac{189}{2*3^6} }=](https://tex.z-dn.net/?f=y%3D+sqrt%5B3%5D%7B-+frac%7Bq%7D%7B2%7D-+sqrt%7BQ%7D%7D%2Bsqrt%5B3%5D%7B-+frac%7Bq%7D%7B2%7D%2B+sqrt%7BQ%7D%7D%3Dsqrt%5B3%5D%7B-+frac%7B61%7D%7B2%2A3%5E6%7D-++frac%7B189%7D%7B2%2A3%5E6%7D+%7D%2Bsqrt%5B3%5D%7B-+frac%7B61%7D%7B2%2A3%5E6%7D%2Bfrac%7B189%7D%7B2%2A3%5E6%7D+%7D%3D)
![=sqrt[3]{frac{-61-189}{2*3^6}}+sqrt[3]{frac{-61+189}{2*3^6}}=sqrt[3]{frac{-250}{2*3^6}}+sqrt[3]{frac{128}{2*3^6}}=sqrt[3]{frac{-125}{3^6}}+sqrt[3]{frac{64}{3^6}}= =sqrt[3]{frac{-61-189}{2*3^6}}+sqrt[3]{frac{-61+189}{2*3^6}}=sqrt[3]{frac{-250}{2*3^6}}+sqrt[3]{frac{128}{2*3^6}}=sqrt[3]{frac{-125}{3^6}}+sqrt[3]{frac{64}{3^6}}=](https://tex.z-dn.net/?f=%3Dsqrt%5B3%5D%7Bfrac%7B-61-189%7D%7B2%2A3%5E6%7D%7D%2Bsqrt%5B3%5D%7Bfrac%7B-61%2B189%7D%7B2%2A3%5E6%7D%7D%3Dsqrt%5B3%5D%7Bfrac%7B-250%7D%7B2%2A3%5E6%7D%7D%2Bsqrt%5B3%5D%7Bfrac%7B128%7D%7B2%2A3%5E6%7D%7D%3Dsqrt%5B3%5D%7Bfrac%7B-125%7D%7B3%5E6%7D%7D%2Bsqrt%5B3%5D%7Bfrac%7B64%7D%7B3%5E6%7D%7D%3D)
![=- sqrt[3]{ frac{5^3}{3^6} } + sqrt[3]{ frac{4^3}{3^6} }=- frac{5}{9} + frac{4}{9} =- frac{1}{9} =- sqrt[3]{ frac{5^3}{3^6} } + sqrt[3]{ frac{4^3}{3^6} }=- frac{5}{9} + frac{4}{9} =- frac{1}{9}](https://tex.z-dn.net/?f=%3D-+sqrt%5B3%5D%7B+frac%7B5%5E3%7D%7B3%5E6%7D+%7D+%2B+sqrt%5B3%5D%7B+frac%7B4%5E3%7D%7B3%5E6%7D+%7D%3D-+frac%7B5%7D%7B9%7D+%2B+frac%7B4%7D%7B9%7D+%3D-+frac%7B1%7D%7B9%7D+)
Корень исходного уравнения
x = y + 4/9 = -1/9 + 4/9 = 3/9 = 1/3
Можно решить и более школьным методом.
3x^3 - 4x^2 + 4x - 1 = 0
3x^3 - x^2 - 3x^2 + x + 3x - 1 = 0
x^2*(3x - 1) - x(3x - 1) + (3x - 1) = 0
(3x - 1)(x^2 - x + 1) = 0
1) 3x - 1 = 0; x = 1/3
2) x^2 - x + 1 = 0
Это уравнение корней не имеет.
Единственный корень x = 1/3, но этот метод подходит не во всех случаях.
Обычное кубическое уравнение.
Решаем методом Кардано. Жаль, что его в школе не проходят.
1) Замена x = y + 4/9. Цель - избавиться от члена x^2
3(y+4/9)^3 - 4*(y+4/9)^2 + 4(y+4/9) - 1 = 0
3(y^3+3*4/9*y^2+3*(4/9)^2*y+(4/9)^3)-4(y^2+2*4/9*y+(4/9)^2)+4y+16/9-1=0
3y^3+4y^2+16/9*y+64/243-4y^2-32/9*y-64/81+4y+16/9-1 = 0
3y^3 + (16/9-32/9+36/9)*y + (64/243-64/81+7/9) = 0
Делим на 3
y^3 + 20/27*y + (64-192+7*27)/243 = 0
y^3 + 20/27*y + 61/729 = 0
Классическое кубическое уравнение вида
y^3 + py + q = 0; где p = 20/27 = 20/3^3; q = 61/729 = 61/3^6
Дискриминант
Корень
Корень исходного уравнения
x = y + 4/9 = -1/9 + 4/9 = 3/9 = 1/3
Можно решить и более школьным методом.
3x^3 - 4x^2 + 4x - 1 = 0
3x^3 - x^2 - 3x^2 + x + 3x - 1 = 0
x^2*(3x - 1) - x(3x - 1) + (3x - 1) = 0
(3x - 1)(x^2 - x + 1) = 0
1) 3x - 1 = 0; x = 1/3
2) x^2 - x + 1 = 0
Это уравнение корней не имеет.
Единственный корень x = 1/3, но этот метод подходит не во всех случаях.
Похожие вопросы
Предмет: Математика,
автор: simaskoila8
Предмет: Информатика,
автор: rajolha
Предмет: Алгебра,
автор: igortaslykov1376
Предмет: Алгебра,
автор: ЛарисаМария
Предмет: Алгебра,
автор: dilyara200297