Предмет: Геометрия,
автор: a1234512345123
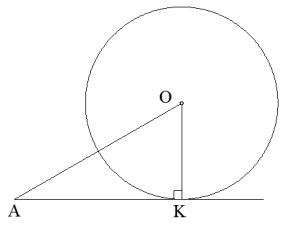
Вычисли радиус окружности, если отрезок касательной
AK=3√3 мм и ∢OAK=30°
OK=?
Приложения:
Ответы
Автор ответа:
0
Треугольник ОАК прямоугольный т.к. радиус, проведенный в точку касания, перпендикулярен к касательной. Т.к. <OAK =30, то ОК=1/2АО или АО=ОК. Пусть ОК=х, тогда АО=2х. по теореме Пифагора АO^2=AK^2+OK^2
4x^2=27+x^2. 3x^2=27. x^2=9. x=3=OK=R
Похожие вопросы
Предмет: Биология,
автор: perets1212
Предмет: Физика,
автор: Gazimov228
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: Katusha2014kd