Предмет: Геометрия,
автор: ovch22
1.Найдите сторону основания и высоту правильной четырехугольной призмы,если её боковая поверхность равна 8 см2 , а полная 40 см2
2.В прямоугольном параллелепипеде стороны основания 7 дм и 24 дм,а высота параллелепипеда 9дм.Найдите площадь диагонального сечения параллелепипеда.
3. в правильной четырехугольной пирамиде двугранный угол при основании
60 ° ,сторона основания- 6 см.Найдите полную поверхность пирамиды.
Ответы
Автор ответа:
0
Две первых задачи решены Пользователем
Maksim2009rus Хорошист
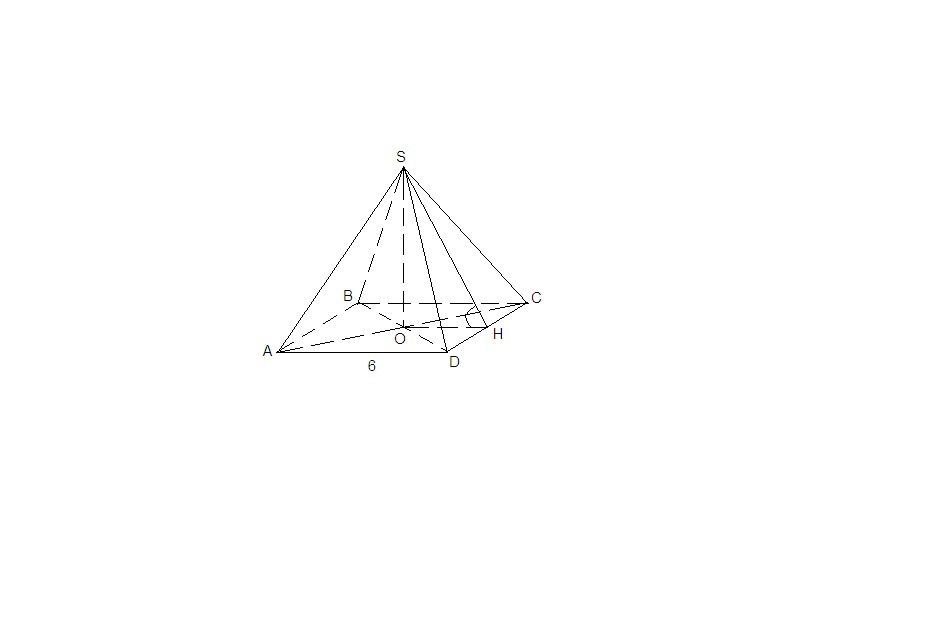
3. Так как пирамида правильная, в основании квадрат, а основание высоты - точка О - точка пересечения диагоналей квадрата.
ОН⊥CD, ОН - проекция SH на основание, значит и SH⊥CD по теореме о трех перпендикулярах. ⇒
∠SHO = 60° - линейный угол двугранного угла при ребре основания.
ОН║AD как перпендикуляры к одной прямой, ⇒ ОН - средняя линия треугольника ACD, ОН = AD/2 = 3 см.
ΔSOH: ∠SOH = 90°,
cos∠SHO = OH/SH
SH = OH / cos60° = 3 / (1/2) = 6 см
Sполн = Sбок + Sосн =
= 0,5Pосн · SH + AD² = 0,5 · 24 · 6 + 36 = 72 + 36 = 108 см²
Maksim2009rus Хорошист
3. Так как пирамида правильная, в основании квадрат, а основание высоты - точка О - точка пересечения диагоналей квадрата.
ОН⊥CD, ОН - проекция SH на основание, значит и SH⊥CD по теореме о трех перпендикулярах. ⇒
∠SHO = 60° - линейный угол двугранного угла при ребре основания.
ОН║AD как перпендикуляры к одной прямой, ⇒ ОН - средняя линия треугольника ACD, ОН = AD/2 = 3 см.
ΔSOH: ∠SOH = 90°,
cos∠SHO = OH/SH
SH = OH / cos60° = 3 / (1/2) = 6 см
Sполн = Sбок + Sосн =
= 0,5Pосн · SH + AD² = 0,5 · 24 · 6 + 36 = 72 + 36 = 108 см²
Приложения:


Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: malakeev12kirill
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: bronnikovi