Предмет: Алгебра,
автор: judooo
найдите разность корней системы уравнений
Приложения:
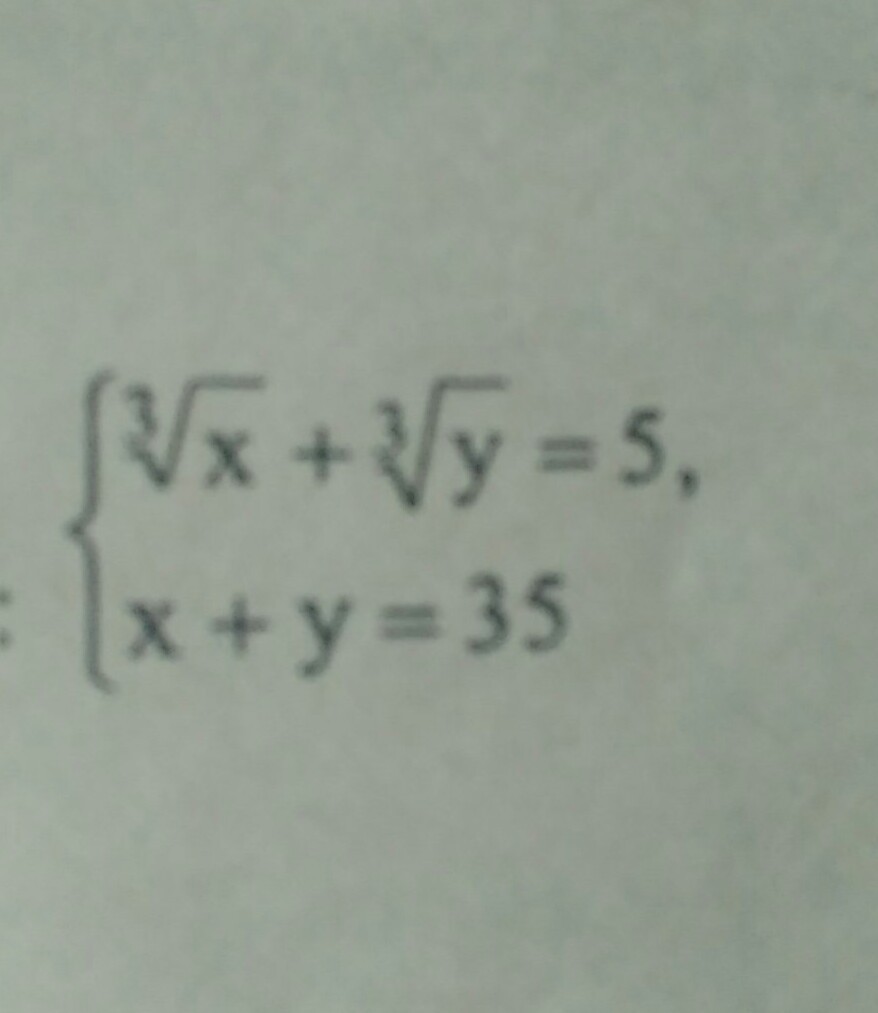
Ответы
Автор ответа:
0
Пусть ∛x = a, ∛y = b.
Тогда система примет вид:

Сумма кубов равна:
a³ + b³ = (a + b)(a² - ab + b²).
Заменим (a + b) = 5, тогда 5(a² - ab + b²) = 35. Сократим на 5:
a² - ab + b² = 7. Сделаем замену b = 5 - а.
a² - a(5 - а) + (5 - а)² = 7. Раскроем скобки:
a² - 5a + а² + 25 - 10а + а² = 7. Приведём подобные и получаем квадратное уравнение 3а² - 15 а + 18 = 0. Сократим на 3:
а² - 5 а + 6 = 0.
Квадратное уравнение, решаем относительно a: Ищем дискриминант:
D=(-5)^2-4*1*6=25-4*6=25-24=1;Дискриминант больше 0, уравнение имеет 2 корня:
a₁=(√1-(-5))/(2*1)=(1-(-5))/2=(1+5)/2=6/2=3;a₂=(-√1-(-5))/(2*1)=(-1-(-5))/2=(-1+5)/2=4/2=2.
Отсюда получаем: х₁ = а³ = 2³ = 8,
х₂ = 3³ = 27,
у₁ = b³ = (5-2)³ = 27,
y₂ = (5-3)³ = 8.
Разность корней системы уравнений равна: 1) 8-27 = -19,
2) 27-8 = 19.
Тогда система примет вид:
Сумма кубов равна:
a³ + b³ = (a + b)(a² - ab + b²).
Заменим (a + b) = 5, тогда 5(a² - ab + b²) = 35. Сократим на 5:
a² - ab + b² = 7. Сделаем замену b = 5 - а.
a² - a(5 - а) + (5 - а)² = 7. Раскроем скобки:
a² - 5a + а² + 25 - 10а + а² = 7. Приведём подобные и получаем квадратное уравнение 3а² - 15 а + 18 = 0. Сократим на 3:
а² - 5 а + 6 = 0.
Квадратное уравнение, решаем относительно a: Ищем дискриминант:
D=(-5)^2-4*1*6=25-4*6=25-24=1;Дискриминант больше 0, уравнение имеет 2 корня:
a₁=(√1-(-5))/(2*1)=(1-(-5))/2=(1+5)/2=6/2=3;a₂=(-√1-(-5))/(2*1)=(-1-(-5))/2=(-1+5)/2=4/2=2.
Отсюда получаем: х₁ = а³ = 2³ = 8,
х₂ = 3³ = 27,
у₁ = b³ = (5-2)³ = 27,
y₂ = (5-3)³ = 8.
Разность корней системы уравнений равна: 1) 8-27 = -19,
2) 27-8 = 19.
Похожие вопросы
Предмет: Физкультура и спорт,
автор: tmtiulgisvili
Предмет: Алгебра,
автор: belozerovanadegda
Предмет: Литература,
автор: spyromarchenko13
Предмет: История,
автор: ksenshik0233
Предмет: Математика,
автор: malchikova