Предмет: Геометрия,
автор: Аноним
Теорема об отрезках касательных к окружности
Ответы
Автор ответа:
0
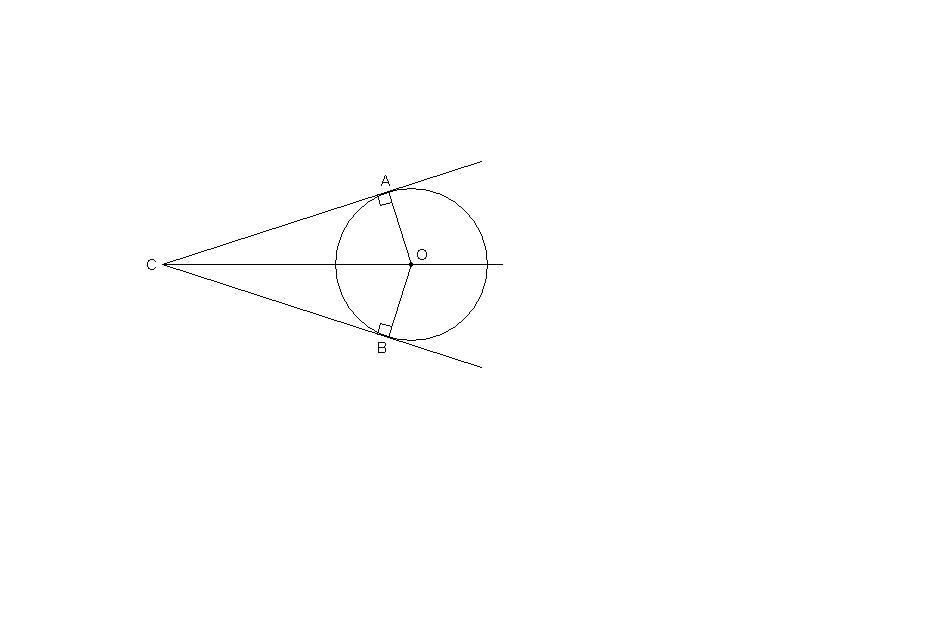
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Доказательство:
Проведем ОА и ОВ - радиусы в точки касания. По свойству касательной, радиус, проведенный в точку касания, перпендикулярен касательной.
В треугольниках ОАС и ОВС:
∠ОАС = ∠ОВС = 90°,
ОА = ОВ как радиусы,
ОС - общая гипотенуза, значит
ΔОАС = ΔОВС по гипотенузе и катету.
Из равенства треугольников следует, что
СА = СВ и
∠АСО = ∠ВСО.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: rajdenprivetetoarami
Предмет: Русский язык,
автор: aaldiyar2903
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: Леночка8888
Предмет: Обществознание,
автор: Termenator228