Предмет: Алгебра,
автор: SAHARIA
Определите A и B так, чтобы Ax^4-Bx^2-6x-3 делился на (x+1)^2
Приложения:
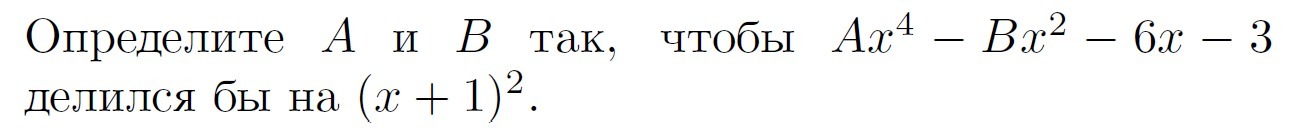
Ответы
Автор ответа:
0
Если многочлен четвертой степени разделить на многочлен второй степени, то получим многочлен второй степени.
(Ах⁴-Вх²-6х-3):(х+1)²=(Mx²+Nx+C)
или
Ах⁴-Вх²-6х-3=(x+1)²·(Mx²+Nx+C)
Ах⁴-Вх²-6х-3=(x²+2x+1)·(Mx²+Nx+C)
Ах⁴-Вх²-6х-3=Mx⁴+Nx³+Cx²+2Mx³+2Nx²+2Cx+Mx²+Nx+C
Ах⁴-Вх²-6х-3=Mx⁴+(N+2M)x³+(C+2N+M)x²+(2C+N)x+C
Два многочлена равны, если степени эти многочлены одной степени и коэффициенты при одинаковых степенях переменной равны.
{ M=A
{N+2M=0
{C+2N+M=-B
{2C+N=-6
{C=-3
N=-6-2C=-6-2·(-3)=0
Тогда N+2M=0
Если N=0, то M=0
C=-B
B=3
A=M=0
О т в е т. А=0; В=3
Тогда
-3х²-6х-3=-3·(х²+2х+1) делится на (х+1)²
в ответе получим -3
(Ах⁴-Вх²-6х-3):(х+1)²=(Mx²+Nx+C)
или
Ах⁴-Вх²-6х-3=(x+1)²·(Mx²+Nx+C)
Ах⁴-Вх²-6х-3=(x²+2x+1)·(Mx²+Nx+C)
Ах⁴-Вх²-6х-3=Mx⁴+Nx³+Cx²+2Mx³+2Nx²+2Cx+Mx²+Nx+C
Ах⁴-Вх²-6х-3=Mx⁴+(N+2M)x³+(C+2N+M)x²+(2C+N)x+C
Два многочлена равны, если степени эти многочлены одной степени и коэффициенты при одинаковых степенях переменной равны.
{ M=A
{N+2M=0
{C+2N+M=-B
{2C+N=-6
{C=-3
N=-6-2C=-6-2·(-3)=0
Тогда N+2M=0
Если N=0, то M=0
C=-B
B=3
A=M=0
О т в е т. А=0; В=3
Тогда
-3х²-6х-3=-3·(х²+2х+1) делится на (х+1)²
в ответе получим -3
Похожие вопросы
Предмет: Русский язык,
автор: genag0096
Предмет: Обществознание,
автор: kvitalina355
Предмет: Математика,
автор: ybydydll
Предмет: Биология,
автор: машенька36
Предмет: Математика,
автор: zaraza121314