Question

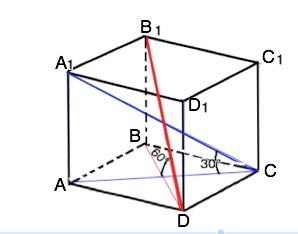
Основание прямой призмы-ромб. Диагонали призмы составляют углы 30 градусов и 60 градусов с плоскостью основания,высота призмы 6 см. Найдите площадь полной поверхности призмы.

Answer 1

Площадь полной поверхности призмы – сумма площади двух оснований и площади боковой поверхности. 

Обозначим вершины призмы ABCDD1A1B1C1

S осн= половине произведения диагоналей. 

АС=АА1:tg30°=6√3

BD=BB1:tg60°=6/√3

S ABCD=6√3•6/√3=36 см*

Площадь боковой поверхности - произведение высоты призмы на периметр основания, т.е. 6•4AB

Ромб - параллелограмм.

В параллелограмме сумма квадратов диагоналей равна сумме квадратов всех его сторон.  Для ромба, стороны которого равны, 

D²+d²=4AB². 

(6√3)²+(6/√3)²=4AB²

AB=√(27+3))=√30

Sбок=6•4√30=24√30см²

S полн=2•36+24√30=24(3+√3)см²