Предмет: Геометрия,
автор: asdfgklp
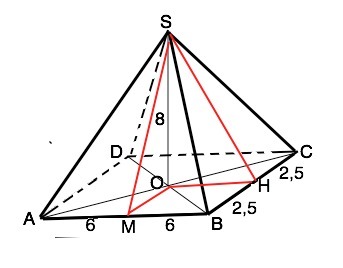
В основании четырехугольной пирамиды SABCD точка O-центр основания ,S-вершина лежит прямоугольник со сторонами 12 см и 5 см.SO=8.Найти площадь боковой и полной поверхности пирамиды.
Ответы
Автор ответа:
0
Основание пирамиды прямоугольник.
Его площадь 12•5=60 см²
Диагонали прямоугольника равны и в точке пересечения делятся пополам ⇒АО=ОВ=ОС=OD. Эти половинки диагоналей - проекции ребер пирамиды. Следовательно, ребра пирамиды как наклонные с равными проекциями равны. SA=SD=SC=SB
Боковые грани – 2 пары равных равнобедренных треугольников с основаниями 12 см и 15 см.
Высота SМ в ∆ASB=√(SO*+OM*)=√(64+6,25)=0,5√281
Высота SН в ∆BSC=√(SO²+OH²)=√(64+36)=10 см
S ∆ASB=AM•SM=6•0,5√281=3√281 см²
S ∆ BSC=BH•SH=2,5•10=25 см²
S бок=2•3√281+2•25=(6√281+50) см² или ≈150,58 см²
S полн=60+60√281+50=(110+60√281) см² или ≈210,58 см²
Приложения:
Похожие вопросы
Предмет: История,
автор: mashka6766
Предмет: Геометрия,
автор: bondarenkonasta02
Предмет: Математика,
автор: vunytka
Предмет: История,
автор: acherevachanna
Предмет: История,
автор: ИванГац