Предмет: Геометрия,
автор: tanyau12001
Сторона правильного треугольника равна 6 корней из 3. Вычислите площадь вписанного в него круга.
Ответы
Автор ответа:
0
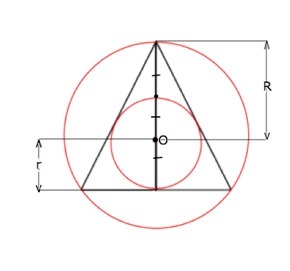
Центр окружности, описанной вокруг треугольника, находится в точке пересечения срединных перпендикуляров.
Центр окружности, вписанной в треугольник, находится в точке пересечения его биссектрис.
Так как срединные перпендикуляры правильного треугольника - его высоты и биссектрисы, центры описанной и вписанной окружности совпадают.
Радиус описанной вокруг правильного треугольника окружности равен 2/3 его высоты.
Радиус вписанной равен половине радиуса описанной окружности, т.е. 1/3 высоты ( медианы, биссектрисы).
Высота правильного треугольника равна (а√3):2, радиус вписанной окружности r=[(а√3):2]:3, где а - сторона треугольника. ⇒
r=[6√3•√3):2]:3=18:6=3
Площадь круга находят по формуле:
S=π•r²
S=π•3²=9π
Центр окружности, вписанной в треугольник, находится в точке пересечения его биссектрис.
Так как срединные перпендикуляры правильного треугольника - его высоты и биссектрисы, центры описанной и вписанной окружности совпадают.
Радиус описанной вокруг правильного треугольника окружности равен 2/3 его высоты.
Радиус вписанной равен половине радиуса описанной окружности, т.е. 1/3 высоты ( медианы, биссектрисы).
Высота правильного треугольника равна (а√3):2, радиус вписанной окружности r=[(а√3):2]:3, где а - сторона треугольника. ⇒
r=[6√3•√3):2]:3=18:6=3
Площадь круга находят по формуле:
S=π•r²
S=π•3²=9π
Приложения:
Похожие вопросы
Предмет: Математика,
автор: svincovaangali
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: moana10
Предмет: Алгебра,
автор: leraowi