Предмет: Алгебра,
автор: raena1
помагите люди пожаулуйста
Приложения:
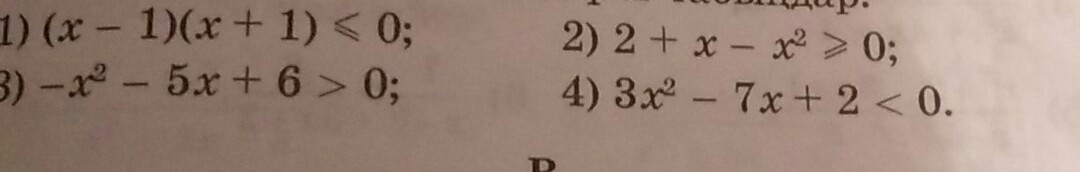
Ответы
Автор ответа:
0
(x - 1)(x + 1) ≤ 0;
x₁ = 1, x₂ = - 1
Интервалы:
(- ∞; - 1]: +
[- 1; 1]: -
[1; + ∞): +
Ответ: [- 1; 1]
2 + x - x² ≥ 0
- x² + x + 2 = 0
x² - x - 2 = 0
x₁ + x₂ = 1
x₁x₂ = - 2
x₁ = 2, x₂ = - 1
(x - 2)(x + 1) ≥ 0
x₁ = 2; x₂ = - 1
Интервалы:
(- ∞; - 1]: +
[- 1; 2]: -
[2; + ∞): +
Ответ: (- ∞; - 1] U [2; + ∞)
- x² - 5x + 6 > 0
x² + 5x - 6 = 0
x₁ + x₂ = - 5
x₁x₂ = - 6
x₁ = 1, x₂ = - 6
(x - 1)(x + 6) > 0
x₁ = 1, x₂ = - 6
Интервалы:
(- ∞; - 6): +
(- 6; 1): -
(1; + ∞): +
Ответ: (- ∞; - 6) U (1; + ∞)
3x² - 7x + 2 < 0
3x² - 7x + 2 = 0
D = (- 7)² - 4 * 3 * 2 = 25
x₁ = (7 + 5) : 6 = 2
x₂ = (7 - 5) : 6 = 1/3
3 (x - 2)(x - 1/3) < 0
x₁ = 2, x₂ = 1/3
Интервалы:
(- ∞; 1/3): +
(1/3; 2): -
(2; + ∞): +
Ответ: (1/3; 2)
x₁ = 1, x₂ = - 1
Интервалы:
(- ∞; - 1]: +
[- 1; 1]: -
[1; + ∞): +
Ответ: [- 1; 1]
2 + x - x² ≥ 0
- x² + x + 2 = 0
x² - x - 2 = 0
x₁ + x₂ = 1
x₁x₂ = - 2
x₁ = 2, x₂ = - 1
(x - 2)(x + 1) ≥ 0
x₁ = 2; x₂ = - 1
Интервалы:
(- ∞; - 1]: +
[- 1; 2]: -
[2; + ∞): +
Ответ: (- ∞; - 1] U [2; + ∞)
- x² - 5x + 6 > 0
x² + 5x - 6 = 0
x₁ + x₂ = - 5
x₁x₂ = - 6
x₁ = 1, x₂ = - 6
(x - 1)(x + 6) > 0
x₁ = 1, x₂ = - 6
Интервалы:
(- ∞; - 6): +
(- 6; 1): -
(1; + ∞): +
Ответ: (- ∞; - 6) U (1; + ∞)
3x² - 7x + 2 < 0
3x² - 7x + 2 = 0
D = (- 7)² - 4 * 3 * 2 = 25
x₁ = (7 + 5) : 6 = 2
x₂ = (7 - 5) : 6 = 1/3
3 (x - 2)(x - 1/3) < 0
x₁ = 2, x₂ = 1/3
Интервалы:
(- ∞; 1/3): +
(1/3; 2): -
(2; + ∞): +
Ответ: (1/3; 2)
Похожие вопросы
Предмет: Математика,
автор: nazerke11110
Предмет: Английский язык,
автор: sofiabutko08
Предмет: Алгебра,
автор: ilamalaev75
Предмет: География,
автор: nellimirobyan