Предмет: Геометрия,
автор: Vlad111111112
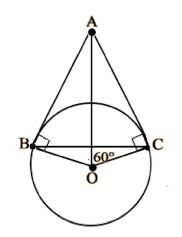
З точки А до кола з центром.У точці О проведенні дотичні АВ і АС (В і С точки дотику).Кут АОС=60 градусів.Довести ,що трикутник АВС рівносторонній. Допоможіть будь-ласка!!!
Ответы
Автор ответа:
0
В треугольнике АОС ОС⊥АС, значит он прямоугольный. ∠САО=90-60=30°.
Касательные, проведённые к окружности из одной точки, равны. АВ=АС.
Прямоугольные треугольники АОС и АОВ равны т.к. ОС=ОВ и АО - общая сторона, значит ∠САО=∠ВАО=30° ⇒ ∠ВАС=60°.
В треугольнике АВС АВ=АС, ∠ВАС=60°, значит ∠АВС=∠АСВ=(180-60)/2=60°, значит ΔАВС правильный (равносторонний).
Доказано.
Касательные, проведённые к окружности из одной точки, равны. АВ=АС.
Прямоугольные треугольники АОС и АОВ равны т.к. ОС=ОВ и АО - общая сторона, значит ∠САО=∠ВАО=30° ⇒ ∠ВАС=60°.
В треугольнике АВС АВ=АС, ∠ВАС=60°, значит ∠АВС=∠АСВ=(180-60)/2=60°, значит ΔАВС правильный (равносторонний).
Доказано.
Автор ответа:
0
Радиус, проведенный в точку касания, перпендикулярен касательной.
∆ АВО и ∆ АСО - прямоугольные с равными катетами ВО=СО и общей гипотенузой АО⇒они равны.
Тогда ∠АОВ=∠АОС=60°
∠ВАО=∠САО=90°-60°=30°⇒∠ВАС=60°
АВ=АС, ∆АВС - равнобедренный, его углы при основании ВС равны, а сумма углов =180°.
⇒∠АВС=∠АСВ=(180°- 60°):2=60°
В треугольнике АВС все углы равны 60°, ⇒ он равносторонний.
∆ АВО и ∆ АСО - прямоугольные с равными катетами ВО=СО и общей гипотенузой АО⇒они равны.
Тогда ∠АОВ=∠АОС=60°
∠ВАО=∠САО=90°-60°=30°⇒∠ВАС=60°
АВ=АС, ∆АВС - равнобедренный, его углы при основании ВС равны, а сумма углов =180°.
⇒∠АВС=∠АСВ=(180°- 60°):2=60°
В треугольнике АВС все углы равны 60°, ⇒ он равносторонний.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: parpievadildaraa
Предмет: Русский язык,
автор: diasbospan
Предмет: Қазақ тiлi,
автор: miras4974
Предмет: Литература,
автор: sasu00