народ,поможете?
в окружности проведены две взаимно перпендикулярные хорды АВ и СД. так что, АД=3 см, а СВ=4 см. найти диаметр.есть фото во вложениях,если кому не понятно условие..
Ответы
Ваш рисунок сделан приблизительно
прямые AD и СВ НЕ обязательно являются параллельными (это частный случай)
вот мое геометрическое построение
следовательно решение через параллельность не является корректным
кроме этого,при параллельности
углы ( ВАD и СВA ) (ВСD и ADC ) накрестлежащие , а их равенство надо еще доказать
рисунок во вложении
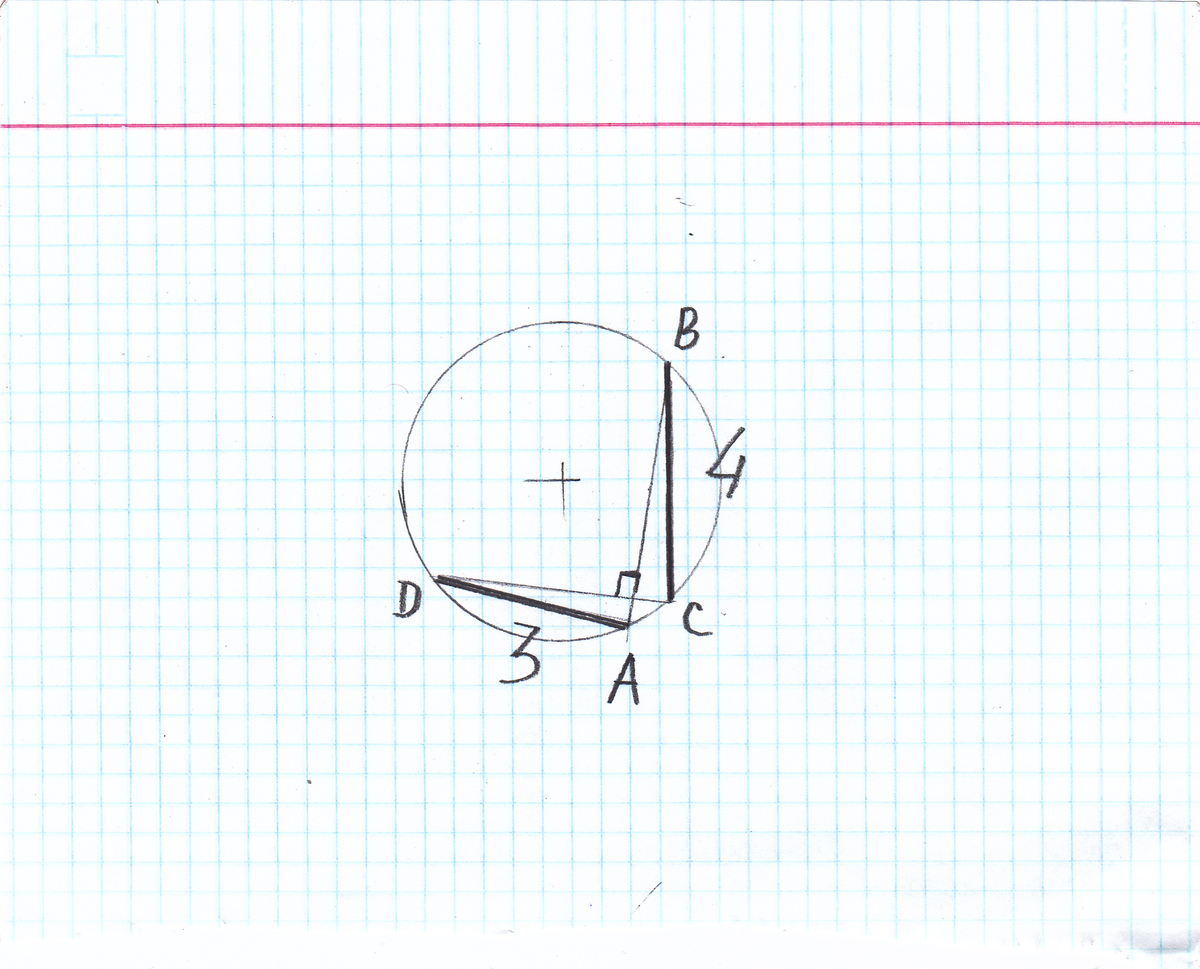
Ваш рисунок заставляет работать мысль в направлении параллельности АД и СВ.
Такое может быть, но вовсе не обязательно.
Поэтому строить решение задачи на этом утверждении не будем.
Сделаем другой рисунок, и из него уже не возникнет мысль о параллелльности АД и СВ.
Желательно открыть рисунок в новом окне, и затем выделить отдельно, чтобы иметь возможность следить за решением по нему.
Помним, что вписанные углы, опирающиеся на равные дуги, равны.
Поэтому опирающиеся на одни и те же дуги
∠ ДАВ=∠ДСВ.
∠ АДС=∠АВС.
Так как треугольники АКД и СКВ прямоугольные ( хорды АВ и СД пересекаются под прямым углом по условию), сумма их острых углов равна 90°
Итак,
имеем два прямоугольных треугольника с равными острыми углами.
В ходе решения мы выяснили:
Сумма углов АДС+ДАВ=90°,
и ∠ АДС=∠ АВС.
Из точки С через центр окружности О проведем диаметр СЕ.
В треугольнике СВЕ ∠ СВЕ= ∠АВС+∠ АВЕ=90° ( ∠ СВЕ опирается на диаметр - дугу 180° и потому он прямой )
Отсюда следует, что ∠АВЕ=∠ДАВ ( дополняют равные углы до 90°),
( Замечу, что для наглядности на рисунке равные углы окрашены в одинаковый цвет, и в сумме голубой и розовый угол дают 90° )
Соединим Е и Д.
Рассмотрим получившийся четырехугольник ВАДЕ.
Он - вписанный, т.к. все его вершины лежат на окружности.
В нем углы А и В при основании АВ равны ( см. выше)
Известно, что
в окружность можно вписать четырехугольник тогда и только тогда, когда сумма его противоположных углов равна 180°.
∠ДАВ +∠ВЕД = 180°, как сумма противоположных углов вписанного четырехугольника,
а так как мы доказали, что ∠ АВЕ=∠ ВАД, то
∠ ВАД+∠АДЕ=180°.
Если при пересечении двух прямых третьей сумма образовавшихся внутренних односторонних углов равна 180°, то прямые параллельны.
( Теперь ясно видно, что не параллельны АД и СВ)
АВ параллельна ДЕ.
Четырехугольник ВАДЕ - трапеция.
Т.к. углы при основании АВ равны, трапеция эта равнобедренная.
АД=ВЕ. ВЕ=3
В прямоугольном треугольнике ВЕС катеты равны 3 и 4.
Треугольник этот - египетский, можно сразу сказать, что диаметр равен 5.
Проверим теоремой Пифагора:
СЕ=√(СВ²+ВЕ²)= √(4²+3²)=5
Ответ: диаметр окружности равен 5
