Решите или найдите решебник пожалуйста!
окружность касается сторон MN и MK прямоугольника MNPK и проходит через вершину p.сторону KP она пересекает в точке a.найдите площадь MNAK,если MN=9,nk=квадратному корню из 145
Ответы
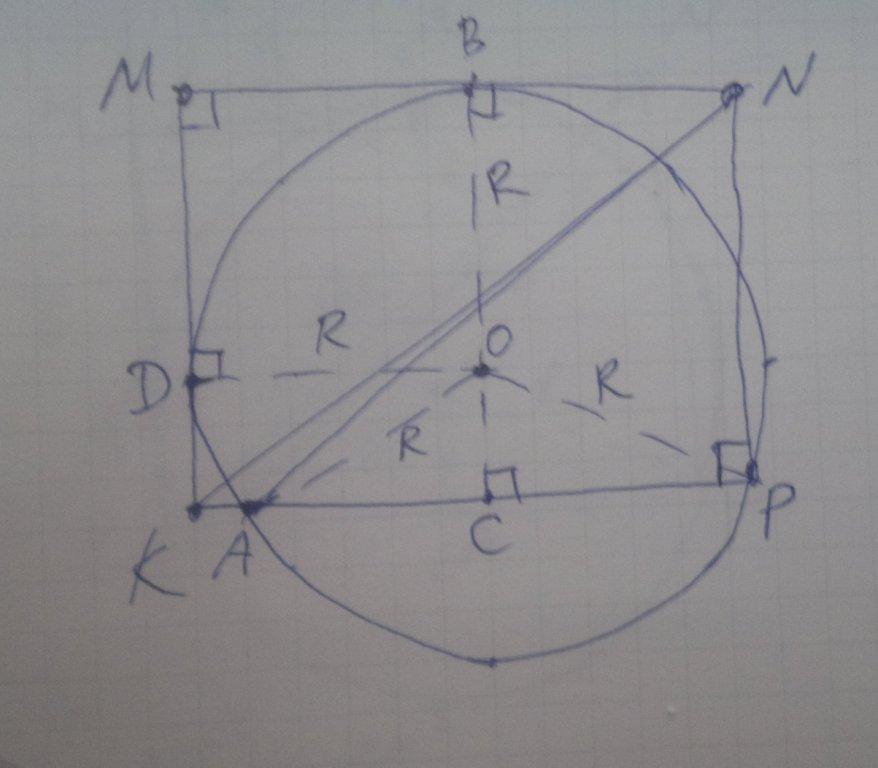
Рисунок во вложении.
MNAK-трапеция.
Площадь трапеции найдем по известной формуле (полусумма оснований умноженная на высоту):
S(MNAK)=((MN+AK)*MK)/2 (1)
MN=9 - нам известна. Нужно найти АK и MK.
MK найдем из прямогульного треугольника MNK.
MK=√(NK²-MN²)=√((√145)²-9²)=8 (2)
Теперь будем искать AK.
AK=PK-AP (3)
AP=2*CP (4)
CP=BN=MN-MB
CP=MN-R=9-R, (5) где R - радиус окружности.
Радиус найдем из прямоугольного треугольника OCP:
R²=OC²+CP² (6)
OC=DK=MK-R=8-R (7)
Подставим (5) и (7) в (6):
R²=(9-R)²+(8-R)² (8)
После преобразования (8) получаем квадратное уравнение:
R²-34R+145=0, корни которого R=5 и R=29
По смыслу задачи нам подходит R=5.
Подставляем R=5 в (5):
CP=9-5=4
Тогда из (4) AP=2*4=8
Из (3) AK=9-8=1
Получаем:
MN=9
AK=1
MK=8
Тогда из (1):
S(MNAK)=((9+1)*8)/2=40
Ответ: S(MNAK)=40