Предмет: Геометрия,
автор: sashka3153
В окружности радиуса 5 проведена хорда длины 8. Большая из окружностей, касающейся данной окружности и хорды имеет площадь?
1. 18пи 2. 16пи 3. 13пи 4. 20пи 5. 5пи корень2
Ответы
Автор ответа:
0
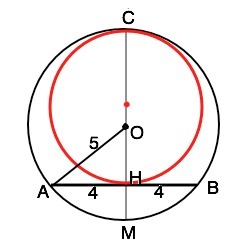
Пусть центр данной окружности О, хорда АВ, диаметр СМ перпендикулярен АВ и пересекает её в середине хорды точке Н. АН=ВН. СО=ОМ - радиусы.
Для второй окружности, хорда АВ - касательная. Следовательно, диаметр СН перпендикулярен АВ и, чтобы быть наибольшим из возможных, должен лежать на диаметре СМ данной окружности.
Соединив О и А, получим прямоугольный ∆ АОН. Этот треугольник -"египетский", катет ОН=3 ( можно проверить по т.Пифагора).
Тогда СН=СО+ОН=5+3=8. Диаметр внутренней окружности СН=8, ее радиус 8:2=4, и S=πr=16π
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: ashlynx123
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: nuriia45
Предмет: Математика,
автор: dias20062