Question

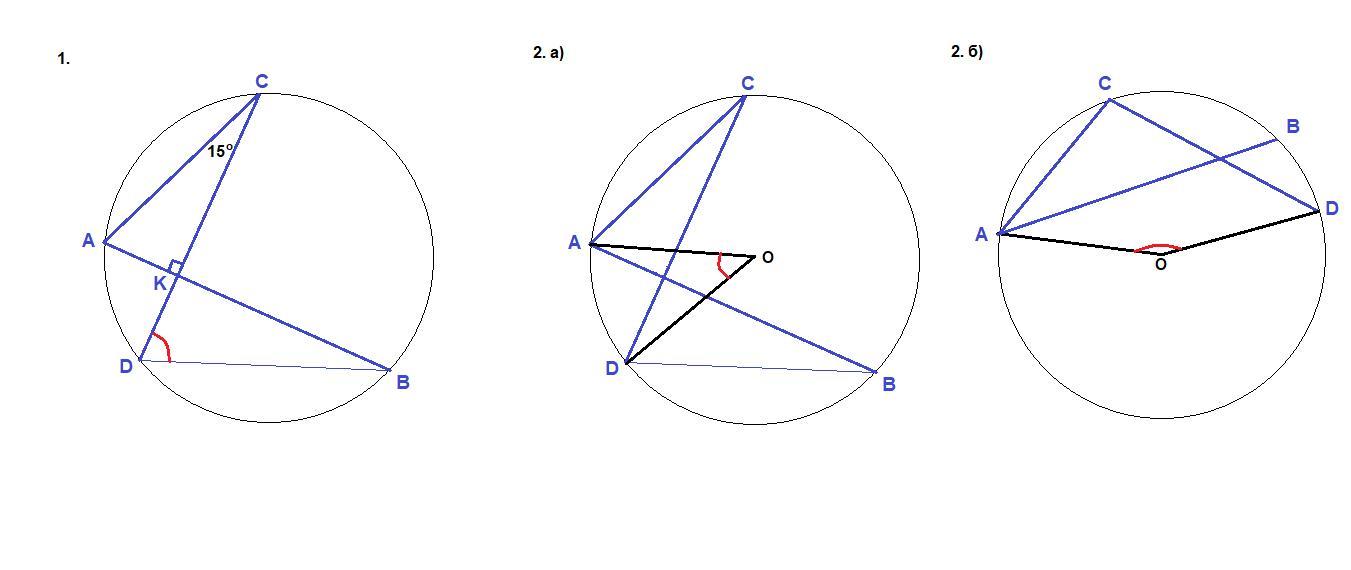
в окружности проведены хорды ав и сд 1. найти угол вдс , если угол асд=15 , ав перпендикулярна сд 2.найт угол аод если а)асд=15 б)угол асд=95

Answer 1

Ответ:

1. ∠BDC = 75°

2. а) ∠AOD = 30°

   б) ∠AOD = 170°

Объяснение:

1. Пусть К - точка пересечения хорд.

ΔАКС: ∠АКС = 90°, ∠АСК = 15°, ⇒

           ∠САК = 90° - 15° = 75°

∠САВ = 75° - вписанный,

∠BDC = ∠CAB = 75° как вписанный, опирающийся на одну дугу с углом САВ.

2.  а) ∠AOD = 2∠ACD = 2 · 15° = 30°, так как вписанный угол равен половине центрального, опирающегося на ту же дугу.

б) ∪AD = 2∠ACD = 2 · 95° = 190°

   ∪ACD = 360° - ∪AD = 360° - 190° = 170°

∠AOD = ∪ACD = 170°, так как центральный угол равен дуге, на которую опирается.