Предмет: Математика,
автор: TheNaik
Вычислить площадь фигуры ограниченной линиями
Приложения:
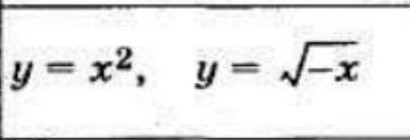
Ответы
Автор ответа:
0
Найдем абсциссы точек пересечения графиков:
Тогда, для нахождения площади нужно вычислить определенный интеграл
Похожие вопросы
Предмет: Математика,
автор: ulanamironec7
Предмет: Алгебра,
автор: Аноним
Предмет: Химия,
автор: pendygat
Предмет: Физика,
автор: Artem1321998
Предмет: История,
автор: Анка2004