Предмет: Математика,
автор: TheNaik
Вычислить определенный интеграл
Приложения:
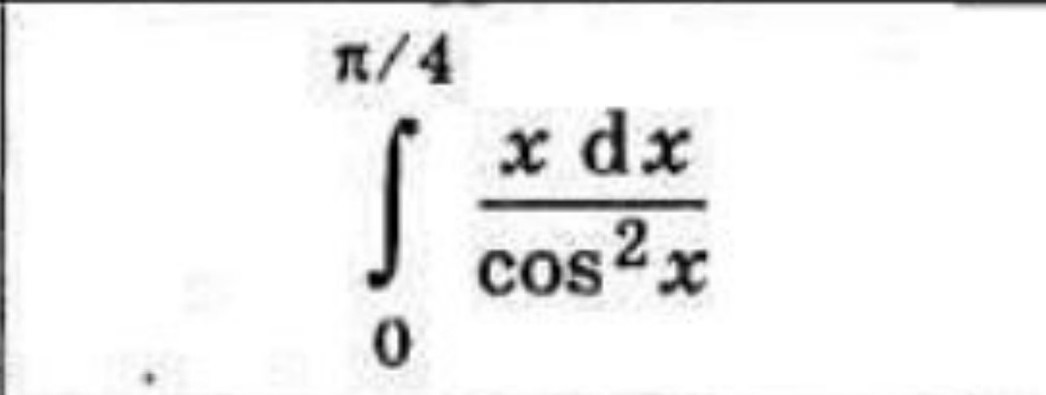
Ответы
Автор ответа:
0
Находим неопределенный интеграл. Интегрируем по частям:
Находим определенный интеграл:
Автор ответа:
0
спасибо
Похожие вопросы
Предмет: Физика,
автор: daria20202
Предмет: Физика,
автор: Аноним
Предмет: Алгебра,
автор: kathdhdhdabockareva7
Предмет: Литература,
автор: рита2310