Предмет: Алгебра,
автор: timursidelnikov
ПОМОГИТЕ, СКОЛЬКО КОРНЕЙ ИМЕЕТ УРАВНЕНИЕ : y = 1/3•x^3 + 2x^2 - 21x - 8
Приложения:

Ответы
Автор ответа:
0
найдем максимумы и минимумы функции y(x)
y'(x)=x²+4x-21
x²+4x-21=0
D=4²+4*21=4(4+21)=4*25
√D=2*5=10
x₁=(-4-10)/2=-7
x₂=(-4+10)/2=3
y(x₁)=y(-7)=(1/3)(-7)³+2*7²-21(-7)-8= 122,7 максимум
y(x₂)=y(3)=(1/3)*3³+2*3²-21*3-8= -44 минимум
y(-∞)=-∞
y(∞)=∞
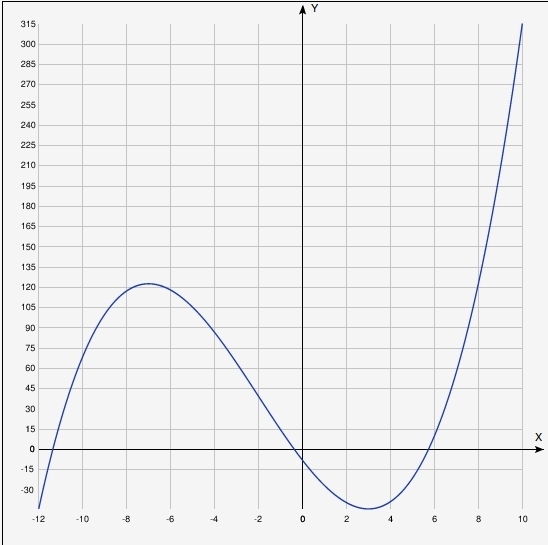
рисуем схематично график функции y(x) (см вложение) и видим, что функция пересекает ось Х в 3 местах
Ответ: 3 корня
Функцию можно не рисовать, а просто рассуждать так:
при x=-∞ y=-∞, дальше по мере увеличения х у тоже растет, чтобы добраться до точки максисмума, в которой функция положительна она дожна пересечь 0 (первый корень), после максимума она дожна придти к минимуму, который отрицательный, для этого ей опять придется пересечь 0 (второй корень), после этого она дожна уйти в +∞ и для этого снова пересечь 0 (третий корень)
y'(x)=x²+4x-21
x²+4x-21=0
D=4²+4*21=4(4+21)=4*25
√D=2*5=10
x₁=(-4-10)/2=-7
x₂=(-4+10)/2=3
y(x₁)=y(-7)=(1/3)(-7)³+2*7²-21(-7)-8= 122,7 максимум
y(x₂)=y(3)=(1/3)*3³+2*3²-21*3-8= -44 минимум
y(-∞)=-∞
y(∞)=∞
рисуем схематично график функции y(x) (см вложение) и видим, что функция пересекает ось Х в 3 местах
Ответ: 3 корня
Функцию можно не рисовать, а просто рассуждать так:
при x=-∞ y=-∞, дальше по мере увеличения х у тоже растет, чтобы добраться до точки максисмума, в которой функция положительна она дожна пересечь 0 (первый корень), после максимума она дожна придти к минимуму, который отрицательный, для этого ей опять придется пересечь 0 (второй корень), после этого она дожна уйти в +∞ и для этого снова пересечь 0 (третий корень)
Приложения:
Автор ответа:
0
спасибо, парень
Автор ответа:
0
вот вопрос есть, можно найти кол-во корней по теореме о корнях, без чертежа?
Автор ответа:
0
честно? не знаю такой теоремы, но может тебе поможет следующая формулировка: если функция монотонно возратает (убывает) на отрезке, то если на границах отрезка она имеет разные знаки, то она имеет на этом отрезке только один корень. у нас тут 3 таких отрезка монотонности функции
Похожие вопросы
Предмет: Русский язык,
автор: utubutubovic201
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: kozklim
Предмет: Математика,
автор: МарияМамаТемы