Предмет: Алгебра,
автор: dte98
Пожалуйста помогите упростить, прошу с решением или объяснением (хочу понять). Спасибо! 
Ответы
Автор ответа:
0
Приложения:
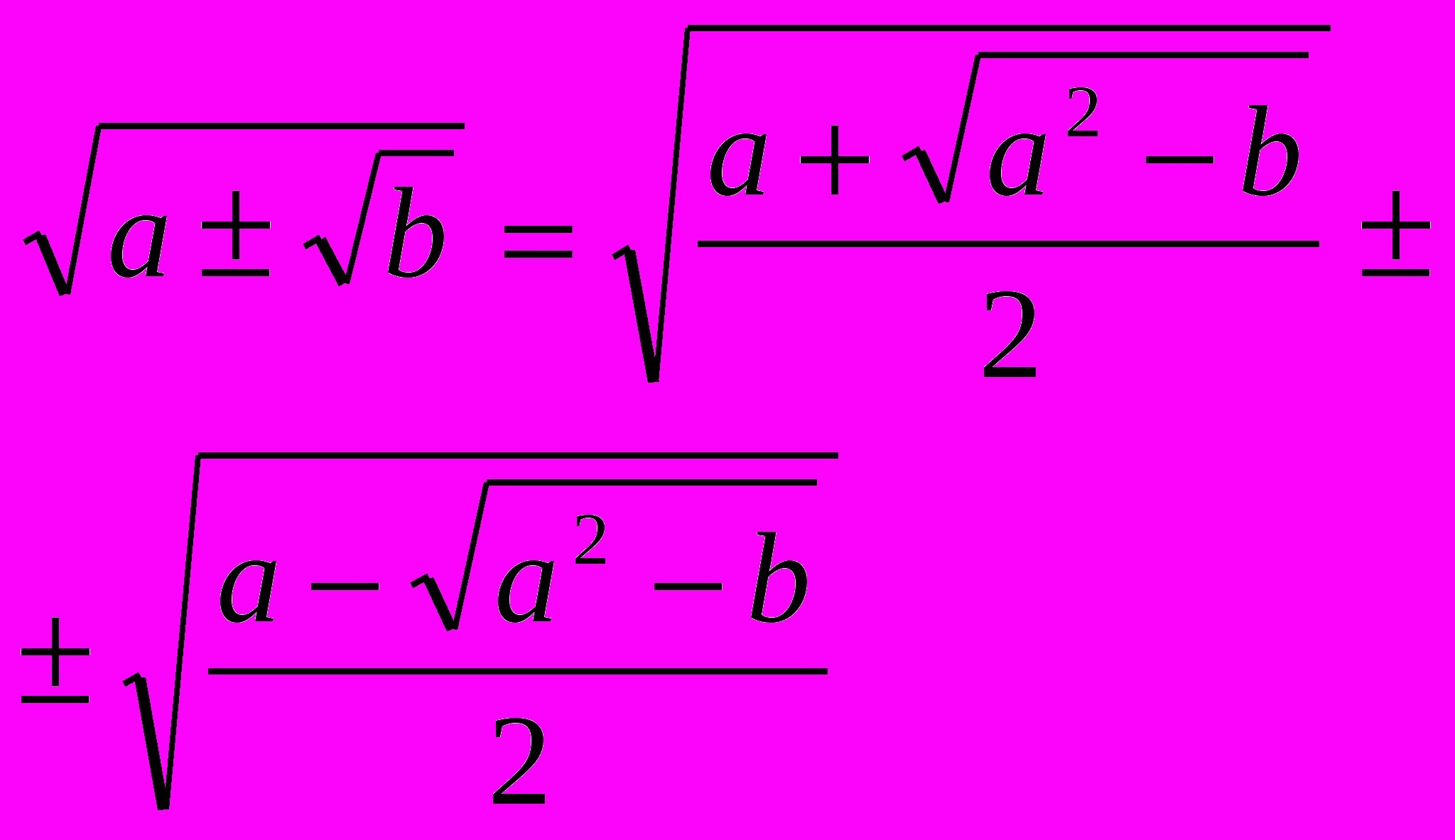
Автор ответа:
0
Огромное спасибо!!! Я понял свою ошибку)
Автор ответа:
0
Приложения:
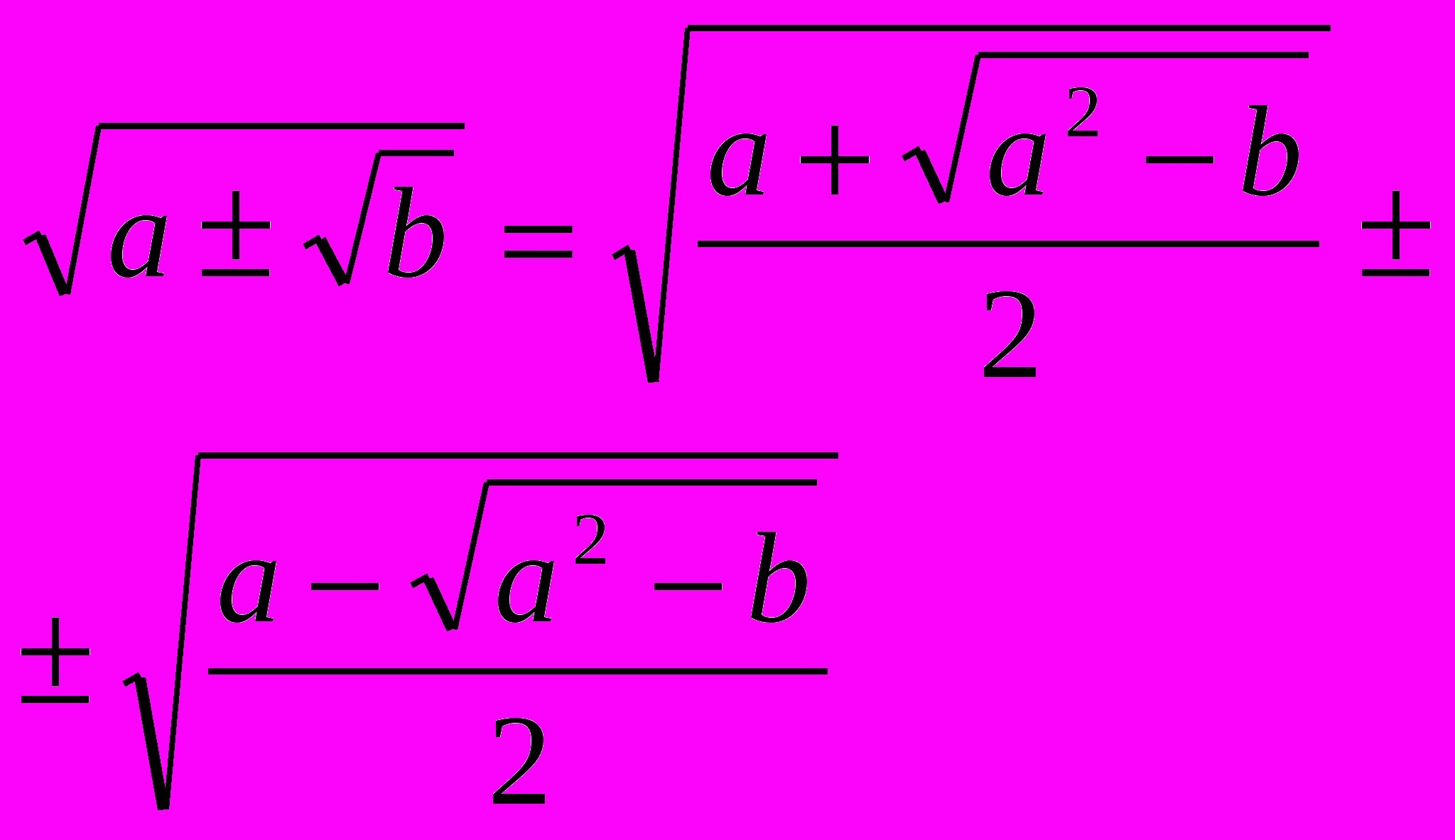
Похожие вопросы
Предмет: Физика,
автор: nowestok
Предмет: География,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: ваня2281
Предмет: Математика,
автор: muradelo