Предмет: Геометрия,
автор: evgeniamelnikov
Геометрия 7 класс. SOS SOS SOS
Приложения:
Ответы
Автор ответа:
0
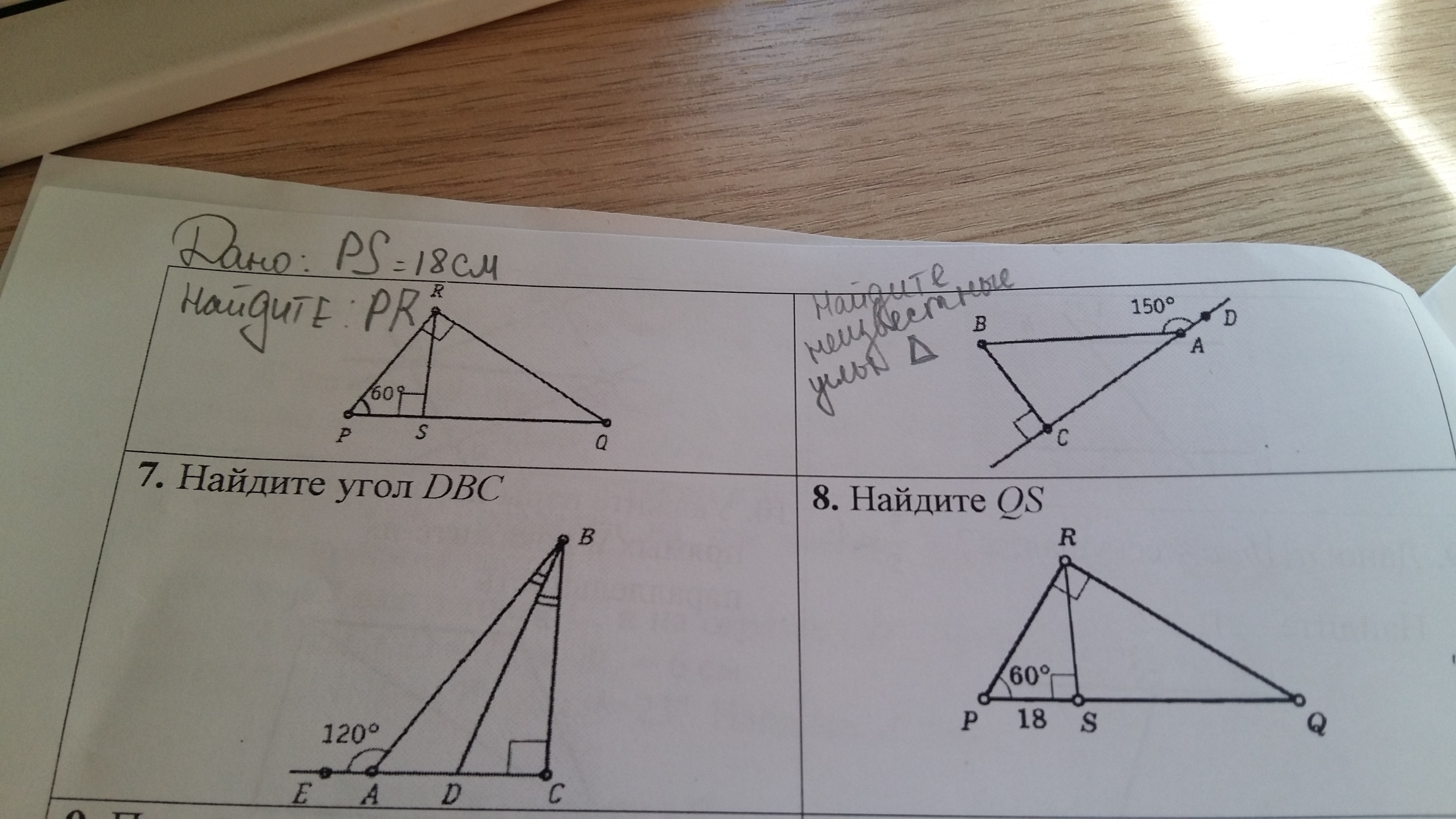
6.
PS = 18
PR = ?
∠RPS = 60
Найдём, с помощью тангенсов. Тангенс угла 60 градусов -
Тангенс прямоугольного треугольника - отношение противолежащего катета к прилижащему.
Первый катет - 18
Второй пускай - a
Тогда

Мы знаем катет 1, катет 2, найдём гипотенузу по Теореме Пифагора:


Ответ: PR = 36 см.
6.
Найдём угол A по теореме о сумме смежных углов.

Угол А = 30
Угол C, опять же, 180 - 90 = 90.
Угол С = 90
Теорема о сумме углов треугольника:
Сума углов треугольника равна 180 градусов.
То есть,
Угол C + Угол A + Угол B = 180
Знаем С и А, подставим
90 + 30 + B = 180
120 + B = 180
B = 180 - 120
B = 60.
Ответ: Угол A равняется 30 градусов, Угол B = 60 градусов, Угол C = 90 градусов.
7
Угол А будет равен 180 - 120, так как Угол EAB и угол CAB смежные.
То есть, угол А = 60 градусов.
Угол C равен 90 градусов.
Сумма углов:
60 + 90 + B = 180
150 + B = 180
B = 180 - 150
B = 30
Так как, BD биссектриса из вершины B, то она разделит угол B пополам. То есть 30 / 2
DBC = 15
Ответ: Угол DBC = 15 Градусов.
8.
Вообще, это задача пипец какая сложная показалась мне, я не знаю что у вас там за 7 класс, но я ели ели решил с помощью синусов, косинусов и теоремы Пифагора, которые проходят в 8 классе, а доходят уже в 9.
Известно что?
Во - первых, мы знаем все углы, все.
Угол P = 60
Угол R = 90
угол Q = 30 (из теоремы про сумму)
Угол S = 90
PS = 18
Можем узнать еще углы SRQ и PRS.
Из теоремы про сумму углов в треугольнике SRQ, узнаём что угол SRQ = 60.
Так как SRQ + PRS = 90, 60 + PRS = 90, PRS = 30
Угол PRS = 30.
Дальше, пускай отрезок PR = t.
Косинус угла 60 градусов = 1 / 2.
cosP = PS/PR
18/t = 1/2
t = 32.
PR = 32 см.
Дальше, по теореме Пифагора:
RS^2 = PR^2 - PS^2
RS^2 = 36^2 - 18^2
RS ^2 = 972
RS =
Дальше по синусу угла Q, так как он равен 30 градусов - синус 30 градусов - 1/2.
Пускай сторона RQ = m
Тогда, sinQ = RS/m

И по теореме Пифагора, находим неизвестный катет.
SQ^2 = RQ^2 - RS^2

Ответ: 54 см длина SQ, можем проверить по теореме Пифагора, будет то же самое)
Ты действительно в 7 классе? Или есть упрощенные теоремы для этой всей писанины? Я не верю..
PS = 18
PR = ?
∠RPS = 60
Найдём, с помощью тангенсов. Тангенс угла 60 градусов -
Тангенс прямоугольного треугольника - отношение противолежащего катета к прилижащему.
Первый катет - 18
Второй пускай - a
Тогда
Мы знаем катет 1, катет 2, найдём гипотенузу по Теореме Пифагора:
Ответ: PR = 36 см.
6.
Найдём угол A по теореме о сумме смежных углов.
Угол А = 30
Угол C, опять же, 180 - 90 = 90.
Угол С = 90
Теорема о сумме углов треугольника:
Сума углов треугольника равна 180 градусов.
То есть,
Угол C + Угол A + Угол B = 180
Знаем С и А, подставим
90 + 30 + B = 180
120 + B = 180
B = 180 - 120
B = 60.
Ответ: Угол A равняется 30 градусов, Угол B = 60 градусов, Угол C = 90 градусов.
7
Угол А будет равен 180 - 120, так как Угол EAB и угол CAB смежные.
То есть, угол А = 60 градусов.
Угол C равен 90 градусов.
Сумма углов:
60 + 90 + B = 180
150 + B = 180
B = 180 - 150
B = 30
Так как, BD биссектриса из вершины B, то она разделит угол B пополам. То есть 30 / 2
DBC = 15
Ответ: Угол DBC = 15 Градусов.
8.
Вообще, это задача пипец какая сложная показалась мне, я не знаю что у вас там за 7 класс, но я ели ели решил с помощью синусов, косинусов и теоремы Пифагора, которые проходят в 8 классе, а доходят уже в 9.
Известно что?
Во - первых, мы знаем все углы, все.
Угол P = 60
Угол R = 90
угол Q = 30 (из теоремы про сумму)
Угол S = 90
PS = 18
Можем узнать еще углы SRQ и PRS.
Из теоремы про сумму углов в треугольнике SRQ, узнаём что угол SRQ = 60.
Так как SRQ + PRS = 90, 60 + PRS = 90, PRS = 30
Угол PRS = 30.
Дальше, пускай отрезок PR = t.
Косинус угла 60 градусов = 1 / 2.
cosP = PS/PR
18/t = 1/2
t = 32.
PR = 32 см.
Дальше, по теореме Пифагора:
RS^2 = PR^2 - PS^2
RS^2 = 36^2 - 18^2
RS ^2 = 972
RS =
Дальше по синусу угла Q, так как он равен 30 градусов - синус 30 градусов - 1/2.
Пускай сторона RQ = m
Тогда, sinQ = RS/m
И по теореме Пифагора, находим неизвестный катет.
SQ^2 = RQ^2 - RS^2
Ответ: 54 см длина SQ, можем проверить по теореме Пифагора, будет то же самое)
Ты действительно в 7 классе? Или есть упрощенные теоремы для этой всей писанины? Я не верю..
Автор ответа:
0
Я просто не знаю, как по другому решать)
Похожие вопросы
Предмет: Английский язык,
автор: runauzumaki299
Предмет: Русский язык,
автор: ima786304
Предмет: Русский язык,
автор: Dameliy13
Предмет: Математика,
автор: ArinaScharova