Предмет: Геометрия,
автор: Taras155
Помогите пожалуйста решить задачу по геометрии очень надо, не игнорьте
За бистрий ответ дам 40 баллов!
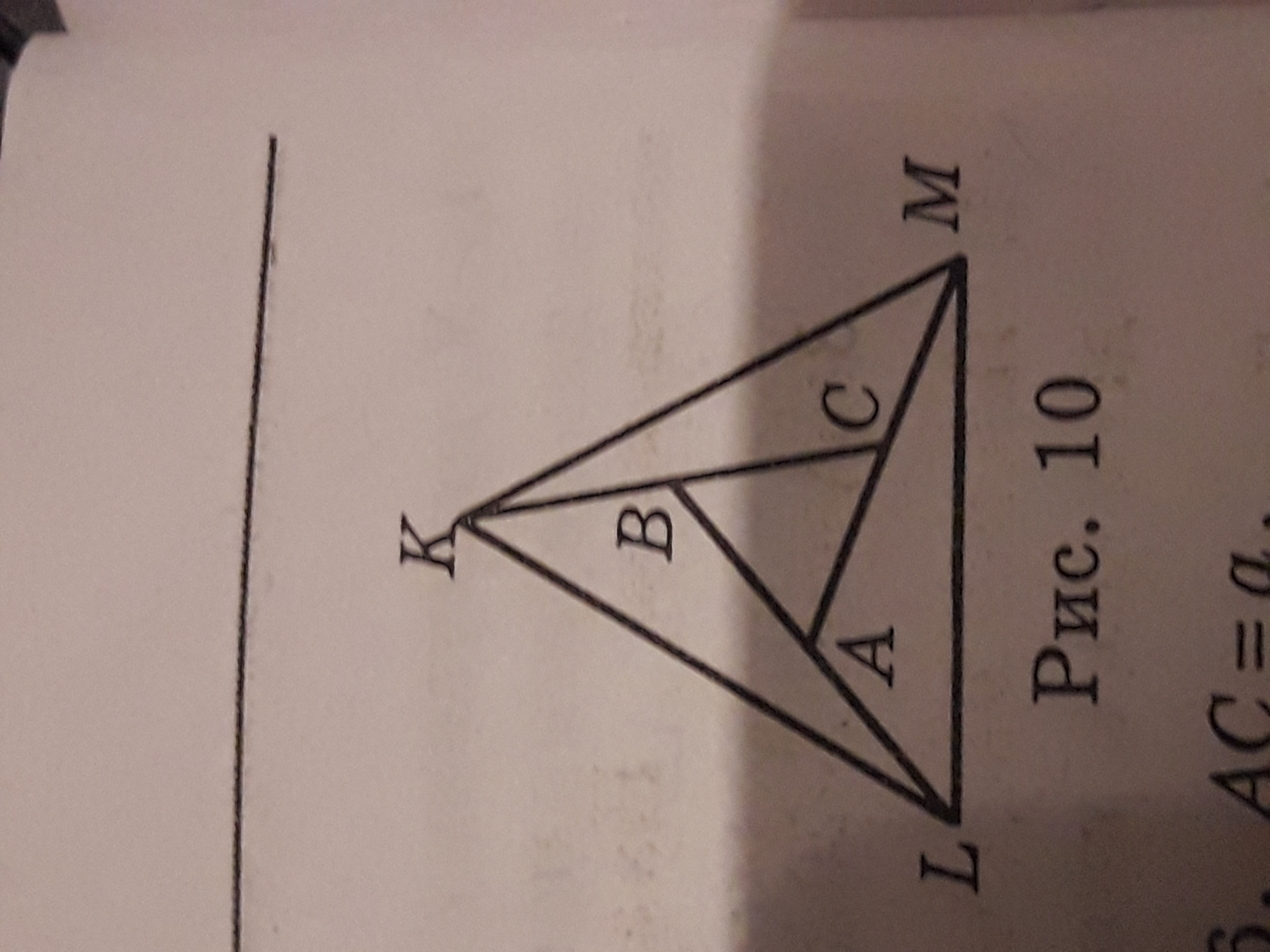
На продолжениях сторон АВ, ВС, АС правильного треугольника АВС отложены отрезки AL, BK, CM так, что AL = BK = CM = AB.
а) Докажите, что треугольник LKM правильный (рис.10, во вложении)
б) Найдите, во сколько раз площадь треугольника LKM больше площади ABC
Приложения:
Ответы
Автор ответа:
0
Смотри 2 не полное прости ну я старался доказательство топовое
Приложения:
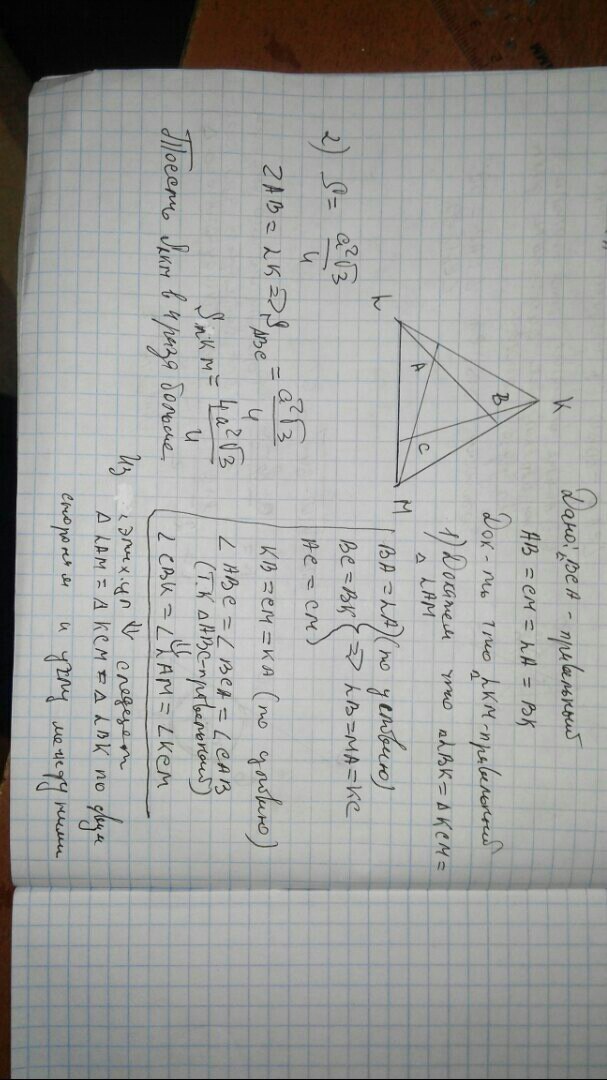
Автор ответа:
0
Обозначим АВ - а;
треугольники KBL, KMA, KBC равны по двум сторонам и углу между ними:
LB=KC=AM=2a; KB=CM=AL=a; ∡А=∡В=∡С=120° - смежные с углами треугольника АВС; ⇒KL=LM=MK ⇒ΔKLM правильный.
SABC=a²sin60°/2;
SKLM=3*SKBL+SABC=3*2a*a*sin120°/2+a²*sin60°/2=(sin120°=sin60°)=
= 7a²*sin60°/2;
Отношение площадей треугольников - 7a²*sin60°/2 : a²sin60°/2 = 7.
треугольники KBL, KMA, KBC равны по двум сторонам и углу между ними:
LB=KC=AM=2a; KB=CM=AL=a; ∡А=∡В=∡С=120° - смежные с углами треугольника АВС; ⇒KL=LM=MK ⇒ΔKLM правильный.
SABC=a²sin60°/2;
SKLM=3*SKBL+SABC=3*2a*a*sin120°/2+a²*sin60°/2=(sin120°=sin60°)=
= 7a²*sin60°/2;
Отношение площадей треугольников - 7a²*sin60°/2 : a²sin60°/2 = 7.
Приложения:

Похожие вопросы
Предмет: Литература,
автор: agaagu71
Предмет: Математика,
автор: timut35diana
Предмет: Другие предметы,
автор: ayanazhubanova
Предмет: Математика,
автор: annakozurova
Предмет: Физика,
автор: Max081198