В правильной усеченной четырехугольной пирамиде площади оснований равны 25 и 9 см2, а боковое ребро образует с плоскостью нижнего основания угол 45 градусов. Вычислить площадь боковой поверхности пирамиды.
Ответы
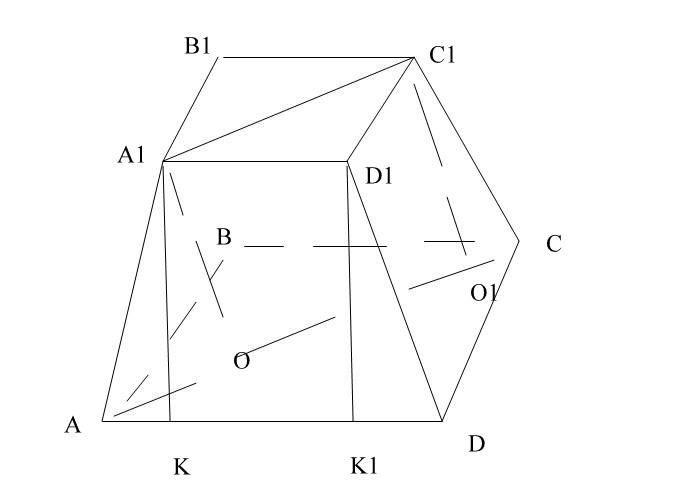
Дана правильная усеченная четырехугольная пирамида ABCDA1B1C1D1.
S ABCD = 25, следовательно сторона квадрата равна 5.
S A1B1C1D1 = 9, следовательно сторона квадрата равна 3.
Проведем диагонали квадратов А1С1 и АС.
Получилась равнобедренная трапеция АА1С1С.
А1С1 = А1В1*корень из 2
А1С1=3 корня из 2
АС = АВ * корень из 2
АС=5 корней из 2.
Проведем высоты А1О и С1О1 трапеции АА1С1С.
ОО1=А1С1=3 корня из 2, следовательно, АО+О1С = 5 корней из 2 - 3 корня из 2.
АО=корень из 2.
Угол А1АО=45 гр., следовательно АО=А1О=корень из 2.
Рассмотрим треугольник АОА1 - прямоугольный.
АА1^2 = AO^2 + A1O^2
AA1=2.
Грани пирамиды - ранобедренные трапеции.
Расмотрим трапецию АА1D1D.
Проведем высоты трапеции А1К и D1K1.
A1D1=KK1=3, следовательно, АК+К1D=5-3=2, АК=1.
Рассмотрим треугольник АКА1-прямоугольный.
А1K^2=AA1^2 - AK^2
A1K = корень из 3.
Sтрап = (A1D1+AD)/2 * A1K = (3+5)/2 * корень из 3 = 4 корня из 3.
Sб.п. = Sтрап * 4 = 4 * 4 корня из 3 = 16 корней из 3