Предмет: Алгебра,
автор: chyolpina
 при
при 
Ответы
Автор ответа:
0
Если дробь имеет смысл (т.е. 2√x≠5√y ), то:
При
Попробуем понять, есть ли какие-то ограничения, все значения возможны. Попробуем найти такие значения, при которых выполняется условие
В общем-то, всё это реально. Но нам именно эти значения невозможны и не нужны.
Итого, правильный ответ: 8, если √y≠8/7, и "в выражении нет смысла", если √y=8/7.
Автор ответа:
0
Решение смотри на фото
Приложения:
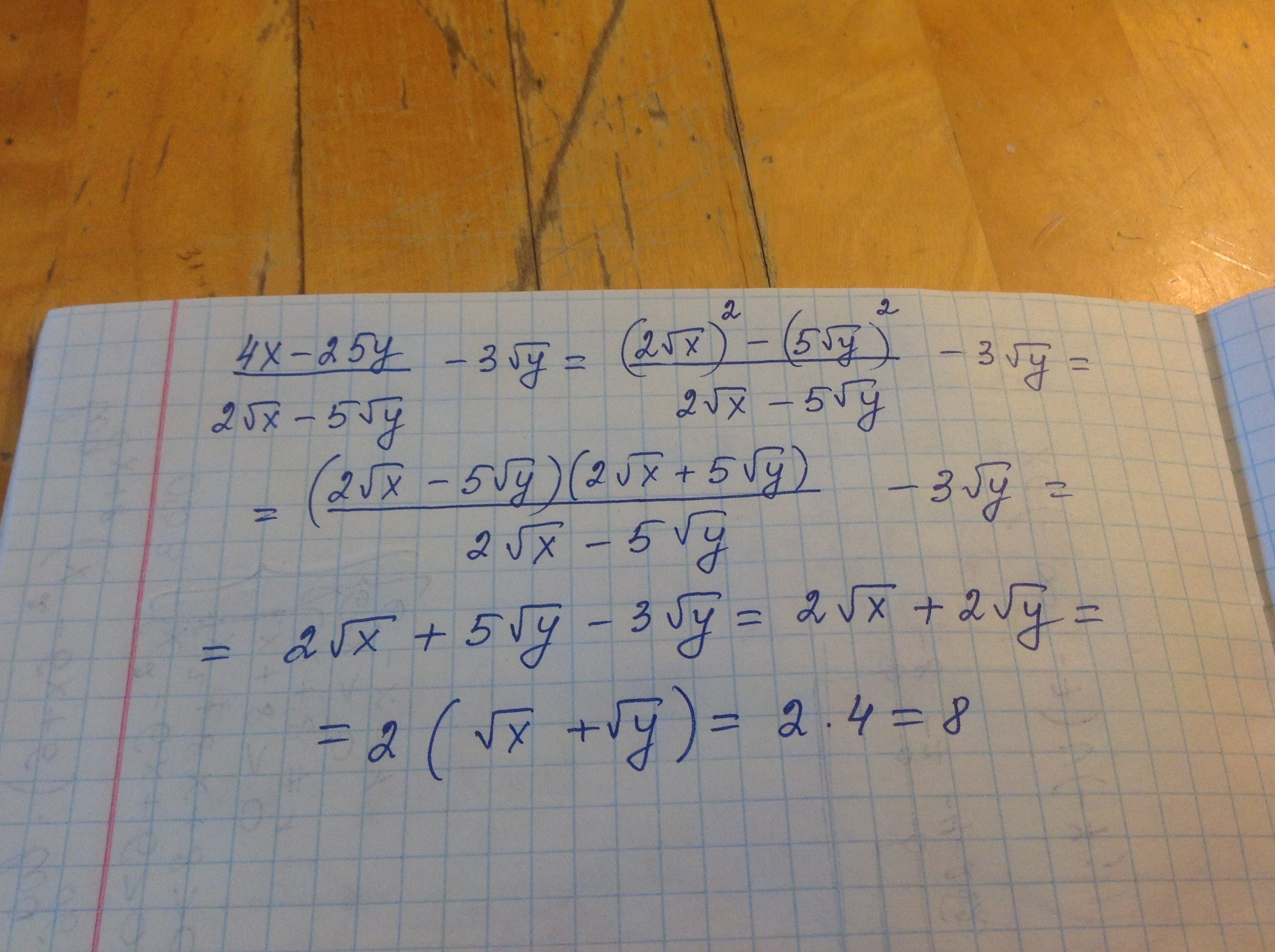
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: egorzaikov03
Предмет: Математика,
автор: Danila291104
Предмет: Математика,
автор: abilovasaniya