Предмет: Алгебра,
автор: Lilanko
sin2x=корень из 2 sin(п/2+х) [-3п;-5п]
Ответы
Автор ответа:
0
sin2x=√2sin(pi/2+х)
2sinxcosx=√2cosx
2sinxcosx-√2cosx=0
cosx(2sinx-√2)=0
cosx=0
x=pi/2+pik, k∈Z
sinx=√2/2
x=pi/4+2pik, k∈Z;
x=3pi/4+2pik, k∈Z
Приложения:
Автор ответа:
0
1)
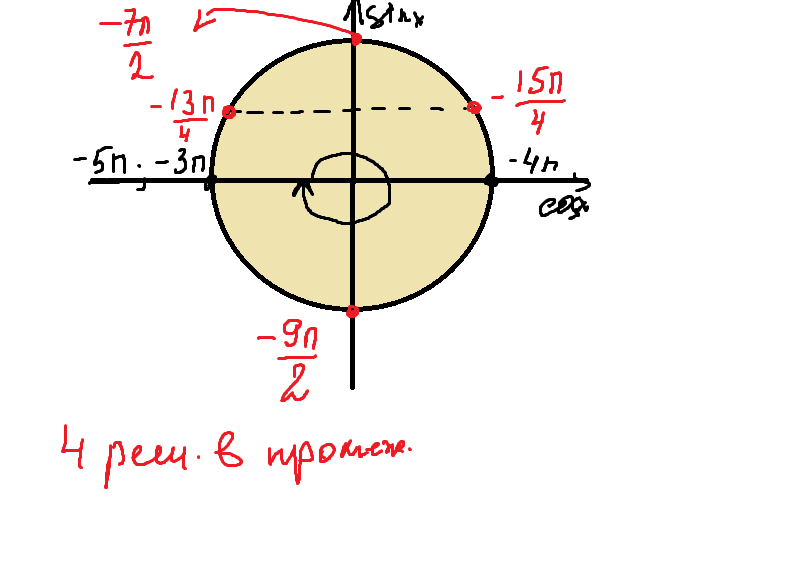
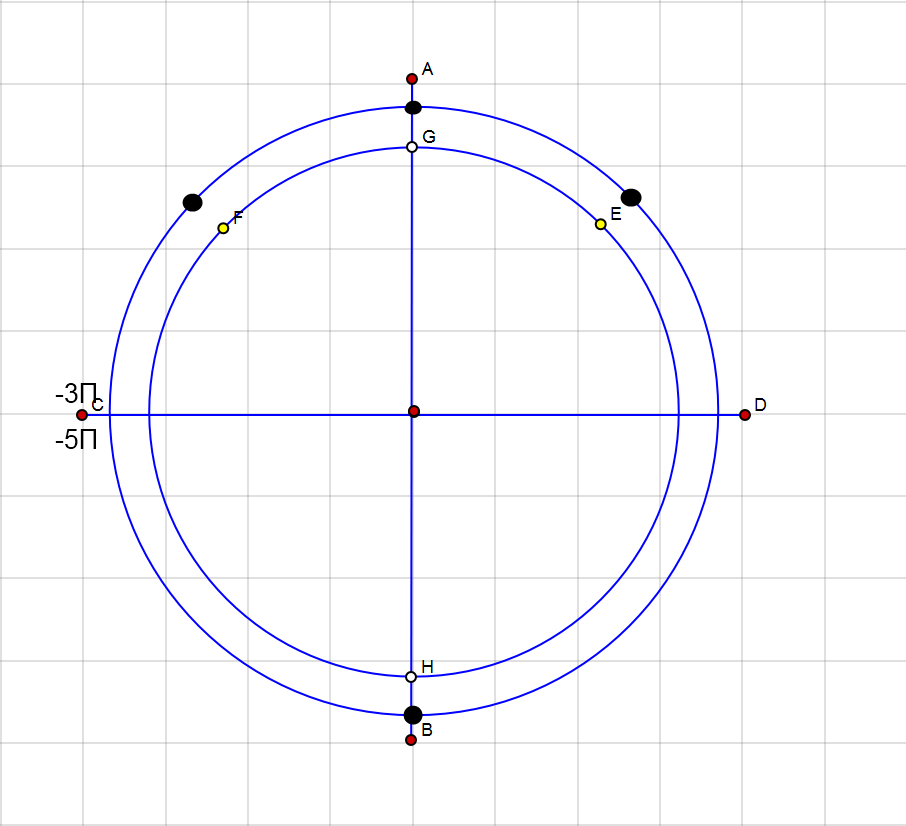
2) [-3п;-5п]
Решения ,которые принадлежат данному отрезку(вложение)
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: agaevmurad2003
Предмет: Английский язык,
автор: melek07aisha
Предмет: Русский язык,
автор: tunuses
Предмет: Физика,
автор: maksimchik31