Question

найдите объем шара,если площадь сечения его плоскостью, удаленной от центра шара на расстояние 6м,равна 64pi м^2

Answer 1

Площадь сечения = πr²

r=√(S/π)=√(64π/π)=8

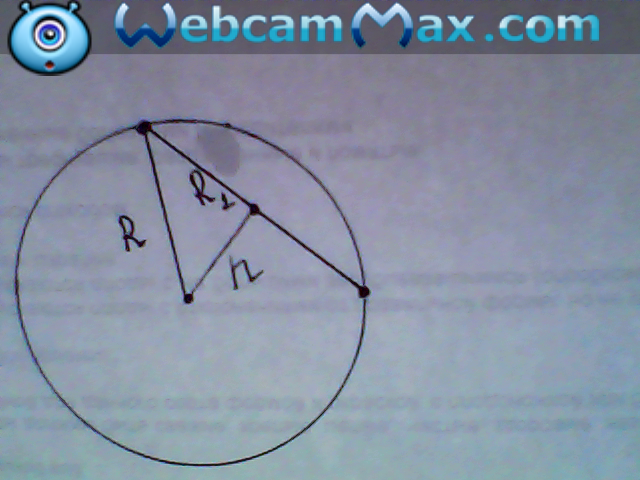
По т Пифагора найдем радиус шара

R²=r²+h²

R=√(8²+6²)=10

V=4/3  *πR³=4/3*π*10³=4000π/3

Answer 2

Так как сечение шара есть окружность, зная ее площадь найдем радиус:

$S=pi R_1^2$

 

$R_1=sqrt{frac{S}{pi}$

 

 $R_1=sqrt{frac{64pi}{pi}}=8$

 

 Тогда исходя из прямоугольного треугольника во вложении находим радуис сферы:

$R=sqrt{h^+R_1^2}=sqrt{6^2+8^2}=10$

 

 Тогда объем сферы равен:

 $V=frac{4}{3}pi R^3=frac{4}{3}*10^3pi=frac{4000}{3}pi$

 

Ответ:  $V=frac{4000}{3}pi$