Question

Нужно решение с рисунком :)

Найдите больший угол треугольника, если две его стороны видны из центра описанной окружности под углами 100° и 120°.

Answer 1

<ABC=½ <AOC

<АОС - центральный угол, он равен градусной мере дуги, на которую опирается.

<АОС=360-120-100=140°

<AOB - вписанный угол, опирается на дугу АС

Вписанный угол равен половине центрального угла

<ABС=½*140=70°

 

Проверка:

<ACB=50°, <BAC=60°

60+50+70=180°

Answer 2

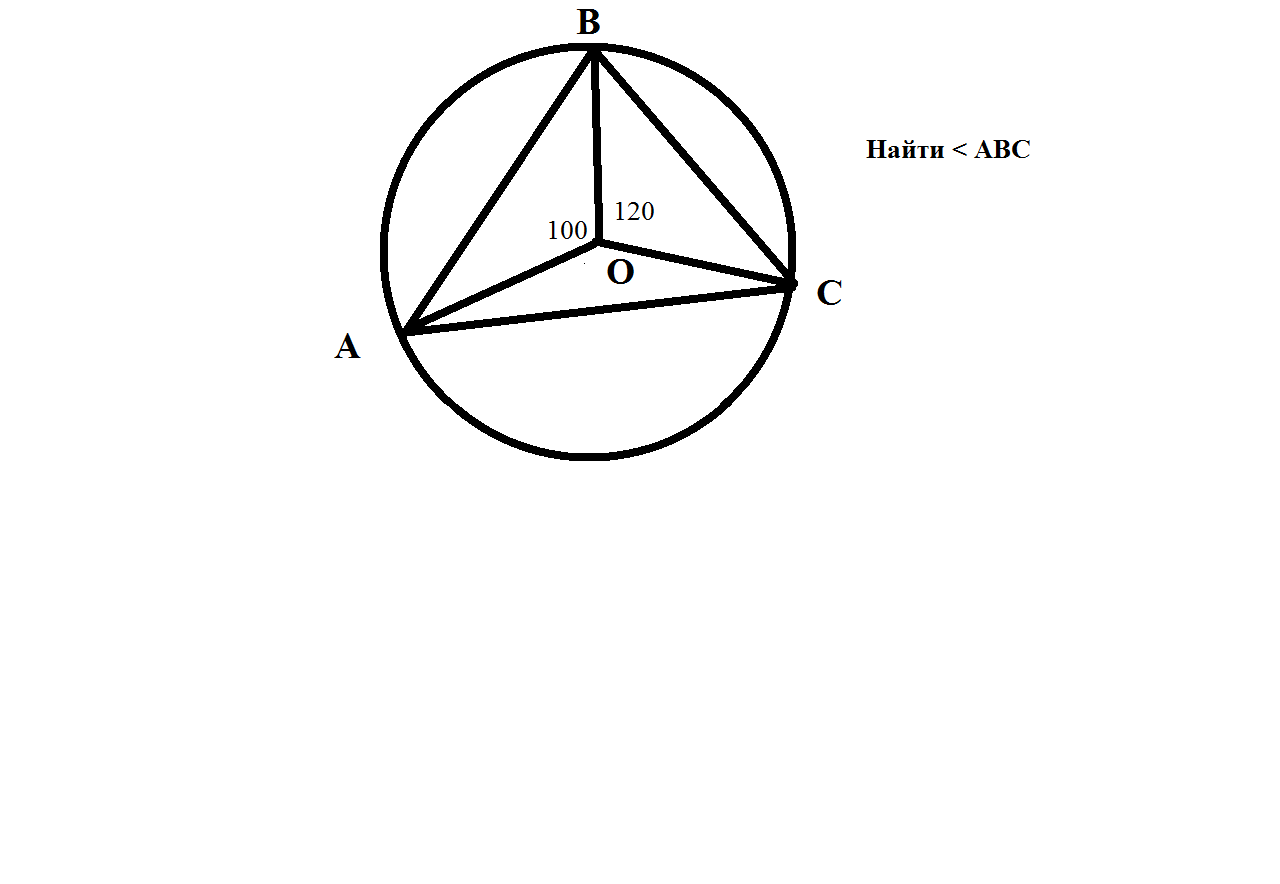
если сказано, что сторона (АВ) видна из центра под углом 100 градусов, это значит, 

что задан центральный угол (АОВ) и он равен 100 градусов и тем самым задан угол 

вписанного треугольника, лежащий против стороны АВ --- угол АСВ 

этот угол вписанный, т.е. он равен половине центрального, опирающегося на ту же дугу, 

т.е. задан угол АСВ в треугольнике АВС и он равен 100/2 = 50 градусов

аналогично рассуждая, получаем второй угол треугольника 120/2 = 60 градусов

очевидно величина третьего угла 180-50-60 = 70 градусов