Предмет: Алгебра,
автор: 1234554321R
log2(x)+20log2x(2)>8
Ответы
Автор ответа:
0
log2(x)+40log2(x)>8
41log2(x)>8
log2(x)>8/41
x.>2^(8/41)
Автор ответа:
0
log_2x+20log_{2x}2>8
ОДЗ: x>0
Вложение.
Приложения:
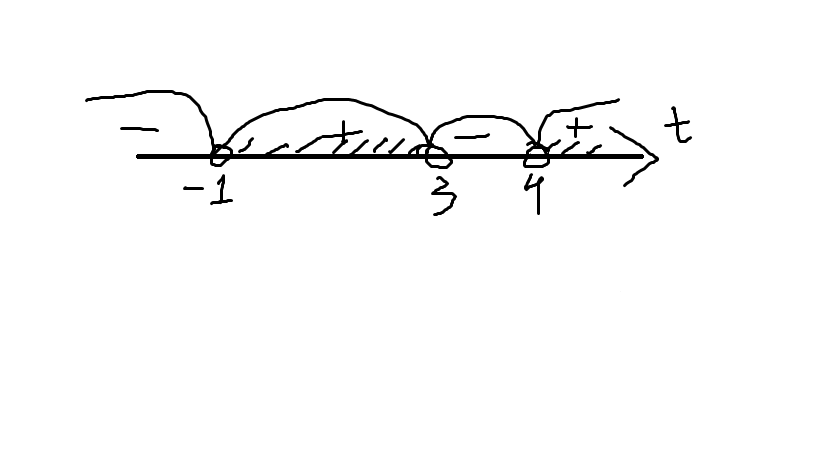
Похожие вопросы
Предмет: Английский язык,
автор: nurayjagypar98
Предмет: Українська література,
автор: mustafaevali723
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: Анонимчик2001
Предмет: Алгебра,
автор: Тамара1999г