Question

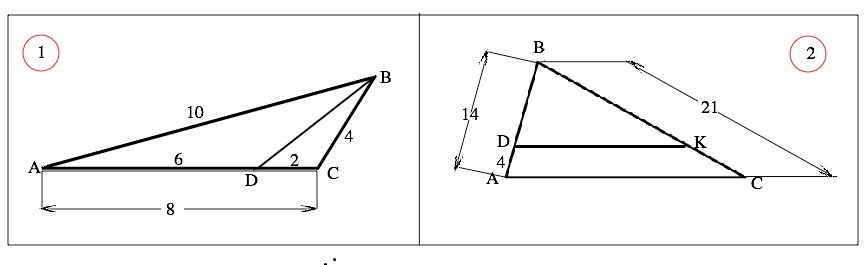
1. В треугольнике ABC известно , что АВ=10 см , ВС=4 см , СА=8 см . На стороне АС отмечена точка D такая , что AD=6 см. Чему равен отрезок BD ?
2. В треугольнике АВС известно , что АВ=14 см , ВС=21 см . На стороне АВ на расстоянии 4 см от вершины А отмечена точка D , через которую проведена прямая , параллельная стороне АС. Найдите отрезки , на которые эта прямая делит сторону BC .
Помогите решить без косинусов т.к мы это еще не проходили

Answer 1

1)  DC=AC-AD=8-6=2 см. Угол С общий для треугольников АВС и DВС, стороны, содержащие этот угол, пропорциональны (АС:ВС=ВС:DC=2). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Из подобия следует АВ:ВD=2, ⇒ BD=10:2=5 см

———————————

2) Обозначим К точку пересечения прямой из т.D с ВС. По условию DK||АС, тогда стороны АВ и ВС треугольника являются секущими для них. ⇒ соответственные углы при DK и АС равны, треугольники АВС и DBK подобны по равным углам. Из подобия следует АВ:DB=ВC:ВK. ВD=AB-AD=10. ⇒ 14:10=21:ВК ⇒ ВК=210:14=15 см. Поэтому  КС=21-15=6 см. Сторона ВС делится на отрезки 15 см и 6 см.