Предмет: Алгебра,
автор: Tanya250
Вычислите
a) Sina, если cos(a+ p/3)=-3/5, P/2< a+P/3<p
b) Cosa, если sin(P/6-a)= 2√2/3, P/2<P/6-a<P
Ответы
Автор ответа:
0
Ответ ответ ответ ответ ответ
Приложения:
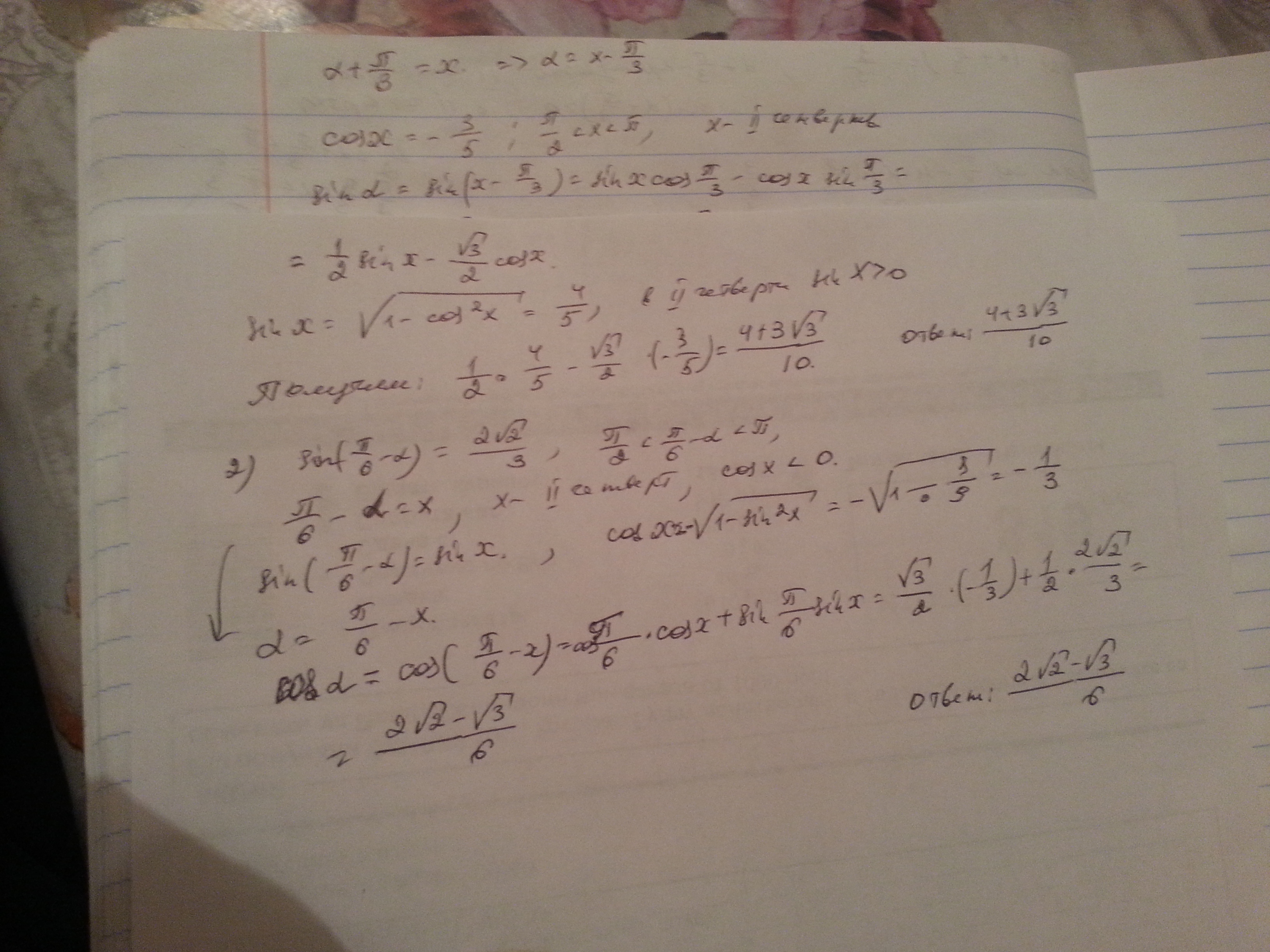

Автор ответа:
0
Вычислите
a) sinα, если cos(α+ π/3)= - 3/5 , π/2 < α+π/3 < π .
---
Т.к. π/2 < α+π/3 < π , то sin(α+ π/3) = √(1-cos²(α+ π/3) =√(1 -(-3/5)² ) = 4/5.
cos(α+ π/3)= - 3/5 ⇔cosα*cosπ/3 - sinα*sinπ/3 = - 3/5⇔
(1/2)*cosα - (√3/2)*sinα = - 3/5 ⇔ -(√3/2)*cosα + (3/2)*sinα = (3√3)/5 (1)
sin(α+ π/3) = 4/5 ⇔sinα*cosπ/3 +cosα*sinπ/3=4/5 ⇔
(√3/2)*cosα +(1/2)*sinα= 4/5 (2)
складывая (1) и (2) получаем:
sinα = (4 +3√3) /10.
-------
b) cosα, если sin(π/6-α)= 2√2/3, π/2<π/6 - α < π .
Т.к. π/2 < π/6 - α < π , то cos(π/6-α) = - √(1- sin² (π/6-α) )= -1/3.
sin(π/6-α)= 2√2/3⇔sinπ/6*cosα -cosπ/6*sinα =2√2/3⇔
(1/2)*cosα - √3/ 2*sinα = 2√2/3 (1) .
cos(π/6-α) = -1/3 ⇔ cosπ/6*cosα+sinπ/6*sinα= -1/3⇔
√3/2*cosα +1/2*sinα = -1/3 ⇔ 3/2*cosα +√3/2*sinα = - √3 /3 (2).
складывая (1) и (2) получаем:
cosα = (2√2 - √3)/ 6 .
a) sinα, если cos(α+ π/3)= - 3/5 , π/2 < α+π/3 < π .
---
Т.к. π/2 < α+π/3 < π , то sin(α+ π/3) = √(1-cos²(α+ π/3) =√(1 -(-3/5)² ) = 4/5.
cos(α+ π/3)= - 3/5 ⇔cosα*cosπ/3 - sinα*sinπ/3 = - 3/5⇔
(1/2)*cosα - (√3/2)*sinα = - 3/5 ⇔ -(√3/2)*cosα + (3/2)*sinα = (3√3)/5 (1)
sin(α+ π/3) = 4/5 ⇔sinα*cosπ/3 +cosα*sinπ/3=4/5 ⇔
(√3/2)*cosα +(1/2)*sinα= 4/5 (2)
складывая (1) и (2) получаем:
sinα = (4 +3√3) /10.
-------
b) cosα, если sin(π/6-α)= 2√2/3, π/2<π/6 - α < π .
Т.к. π/2 < π/6 - α < π , то cos(π/6-α) = - √(1- sin² (π/6-α) )= -1/3.
sin(π/6-α)= 2√2/3⇔sinπ/6*cosα -cosπ/6*sinα =2√2/3⇔
(1/2)*cosα - √3/ 2*sinα = 2√2/3 (1) .
cos(π/6-α) = -1/3 ⇔ cosπ/6*cosα+sinπ/6*sinα= -1/3⇔
√3/2*cosα +1/2*sinα = -1/3 ⇔ 3/2*cosα +√3/2*sinα = - √3 /3 (2).
складывая (1) и (2) получаем:
cosα = (2√2 - √3)/ 6 .
Приложения:
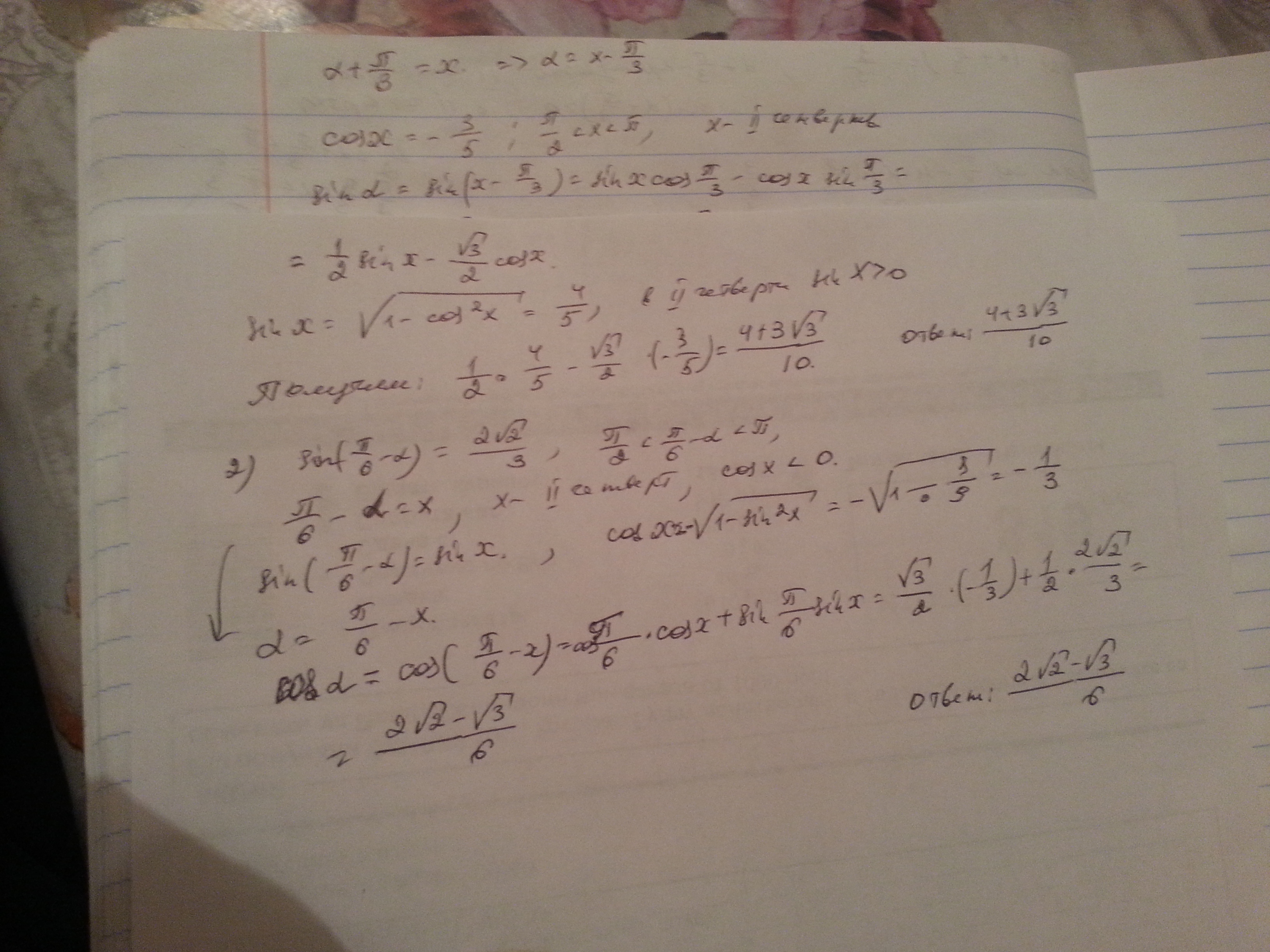

Похожие вопросы
Предмет: Қазақ тiлi,
автор: ailitanabet
Предмет: Биология,
автор: 2052008max
Предмет: Қазақ тiлi,
автор: arujansarsenbinova
Предмет: Обществознание,
автор: malinkaarinka7539