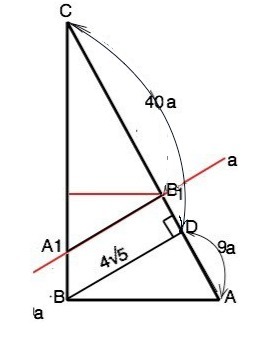
В прямоугольном треугольнике ABC ( B=90°) отрезок BD-высота, проведённая к стороне AC, AD:DC=9:40, BD=4√5.Прямая a, параллельная высоте BD, делит треугольник ABC на две равновеликие части. Найдите длину отрезка прямой a, заключенного между сторонами треугольника ABC
Ответы
Пусть прямая а пересекает АС в т.В1, ВС в т.А1.
А1В1 делит ∆ АВС на две равновеликие части, т. е. на треугольник и четырехугольник равной площади.
S ∆ А1B1C=S BАB1А1= S ∆ABC:2
Прямоугольные треугольники с общим острым углом подобны.
∆ CA1B1~ ∆ СAB.
Площади подобных фигур относятся как квадраты отношения линейных размеров их сходственных элементов.
k²=2 ⇒ k=√2
АВ:А1В1=√2 ⇒ A1B1=AB:√2
АВ найдем из ∆ АВD.
Примем коэффициент отношения отрезков AD:CD равным х.
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
Т.е. ВD² =АD•CD
Тогда 80=40•9x²
9х²=2⇒ х=(√2)/3 и AD=9•(√2)/3 =3√2
Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
АВ²= BD²+AD²
АВ=√(80+9•2)=√49•2=7√2 ⇒ A1B1=7√2:√2=7