Предмет: Математика,
автор: natashaleskovets
Помогииите прошууу!!!!!!
Приложения:
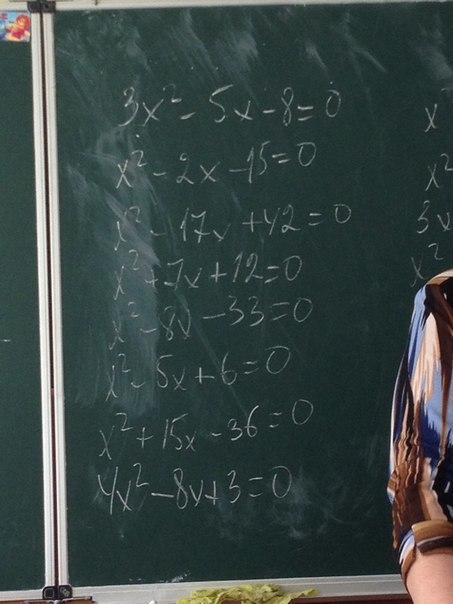

Ответы
Автор ответа:
0
1) можно решить через дискриминант:
D = b² - 4ac
x₁ = ; x₂ =
; x₂ = 
Пример:
3x² - 5x - 8 = 0
D = 25 -4·(-8·3) = 121; = 11
= 11
x₁ = = 8/3
= 8/3
x₂ = = -1
= -1
но это не удобно
2) можно решить через дискриминант/4:
D₁ = ² - ac
² - ac
x₁ = ; x₂ =
; x₂ = 
Пример:
x² - 2x - 15 = 0
D₁ = 1 + 15 = 16; = 4
= 4
x₁ = 1 + 4 = 5
x₂ = 1 - 4 = -3
это чуть-чуть удобнее
3) можно решить через теорему Виета:
x₁ + x₂ = -b; x₁x₂ = c
Пример 1:
x² - 17x + 42 = 0
42 = 7·6 = 14·3
17 = 14 + 3
x₁ = 14; x₂ = 3
Пример 2:
x² + 7x + 12 = 0
12 = 3·4 = -3·(-4)
-7 = -3 + (-4)
x₁ = -3; x₂ = -4
Пример 3:
x² - 8x - 33 = 0 (если перед с стоит минус то у меньшего корня знак b)
33 = 11·3 (у меньшего минус)
8 = -3 + 11
x₁ = -3; x₂ = 11
Пример 4:
x² - 5x + 6 = 0
6 = 6·1 = 3·2
5 = 3 + 2
x₁ = 3; x₂ = 2
Пример 5:
x² + 15x - 36 = 0
36 = 6·6 = 12·3
-15 = -12 - 3
x₁ = -3; x₂ = -12
3)можно решать через обобщённую теорему Виета:
x₁ + x₂ = ; x₁x₂ =
; x₁x₂ = 
но проще так: раскладываем a·c на такие множители м₁ м₂ которые в сумме дают -b:
a·c = м₁·м₂, м₁ + м₂ = -b
x₁ = ; x₂ =
; x₂ = 
Пример:
4x² - 8x + 3 = 0
4·3 = 6·2
8 = 6 + 2
x₁ = ; x₂ =
; x₂ = 
Пример 2:
3x² - 5x - 8 = 0
3·8 = 3·8 (у меньшего минус)
5 = 8 -3
x₁ = ; x₂ =
; x₂ =  = -1
= -1
D = b² - 4ac
x₁ =
Пример:
3x² - 5x - 8 = 0
D = 25 -4·(-8·3) = 121;
x₁ =
x₂ =
но это не удобно
2) можно решить через дискриминант/4:
D₁ =
x₁ =
Пример:
x² - 2x - 15 = 0
D₁ = 1 + 15 = 16;
x₁ = 1 + 4 = 5
x₂ = 1 - 4 = -3
это чуть-чуть удобнее
3) можно решить через теорему Виета:
x₁ + x₂ = -b; x₁x₂ = c
Пример 1:
x² - 17x + 42 = 0
42 = 7·6 = 14·3
17 = 14 + 3
x₁ = 14; x₂ = 3
Пример 2:
x² + 7x + 12 = 0
12 = 3·4 = -3·(-4)
-7 = -3 + (-4)
x₁ = -3; x₂ = -4
Пример 3:
x² - 8x - 33 = 0 (если перед с стоит минус то у меньшего корня знак b)
33 = 11·3 (у меньшего минус)
8 = -3 + 11
x₁ = -3; x₂ = 11
Пример 4:
x² - 5x + 6 = 0
6 = 6·1 = 3·2
5 = 3 + 2
x₁ = 3; x₂ = 2
Пример 5:
x² + 15x - 36 = 0
36 = 6·6 = 12·3
-15 = -12 - 3
x₁ = -3; x₂ = -12
3)можно решать через обобщённую теорему Виета:
x₁ + x₂ =
но проще так: раскладываем a·c на такие множители м₁ м₂ которые в сумме дают -b:
a·c = м₁·м₂, м₁ + м₂ = -b
x₁ =
Пример:
4x² - 8x + 3 = 0
4·3 = 6·2
8 = 6 + 2
x₁ =
Пример 2:
3x² - 5x - 8 = 0
3·8 = 3·8 (у меньшего минус)
5 = 8 -3
x₁ =
Автор ответа:
0
надо подправить
Похожие вопросы
Предмет: Русский язык,
автор: didikrkem
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: prostodryg3978
Предмет: Математика,
автор: sss39