Предмет: Алгебра,
автор: Alegosa
Помогите доказать тождество, пожалуйста
(1-2sin^2x)/(cosx+sinx)+(1-2cos^2x)/(sinx+cosx)=2cosx
Приложения:
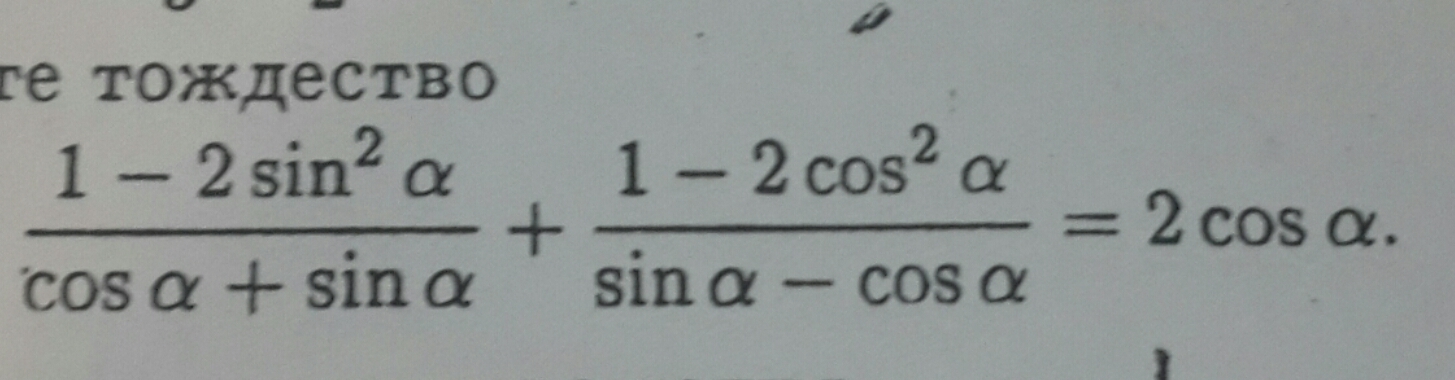
Ответы
Автор ответа:
0
...((sinx-cosx)*(1-2sinx^2)+(cosx+sinx)*(1-2cosx^2))/((cosx+sinx)*(sinx-cosx))=
=(2cosxsinx^2-2cosx^3)/((cosx+sinx)*(sinx-cosx))=(2cosx(sinx-cosx)*(sinx+cosx))/((cosx+sinx)*(sinx-cosx)=2cosx
2cosx=2cosx
=(2cosxsinx^2-2cosx^3)/((cosx+sinx)*(sinx-cosx))=(2cosx(sinx-cosx)*(sinx+cosx))/((cosx+sinx)*(sinx-cosx)=2cosx
2cosx=2cosx
Похожие вопросы
Предмет: Алгебра,
автор: fornogxxx2007
Предмет: Английский язык,
автор: amankozhabauyrzhan55
Предмет: Математика,
автор: trykyn
Предмет: Математика,
автор: tanyklass
Предмет: Математика,
автор: Dimas211d