Помогите решить пожалуйста :)))
1. Для функции f(x) = 4 sin 2x найдите первообразную, график который проходит через точку M ( П/3 ; 1)
2. Lg (3x - 1) - Lg x < Lg 0.6
3. В правильной четырехугольной пирамиде высота равна 8 см, двугранный угол при основании пирамиды равен 30 градусов. Найти объем пирамиды.
4. Площадь боковой поверхности конуса равна 20п см^2, а площадь его основания на 4п с^2 меньше. Найдите объем конуса.
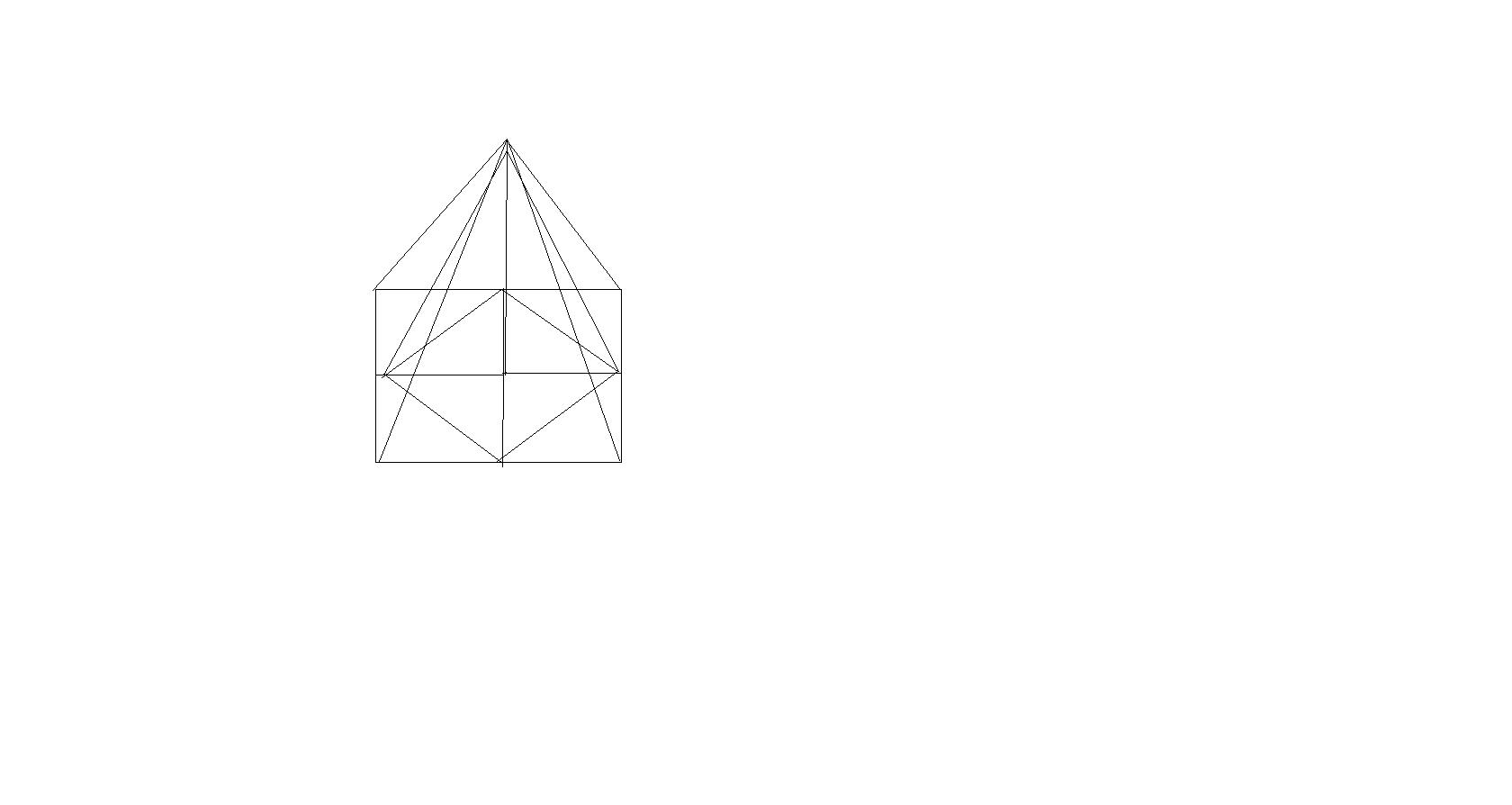
5. Вершинами многогранника являются середины сторон основания и середина высоты правильной четырехугольной пирамиды. Как называется этот многогранник? Сделайте рисунок и отметьте равные ребра этого многогранника.
Ответы
1) первообразная будет иметь вид
F(x)=-2cos2x+C
теперь через точки М(pi/3; 1)
1=-2cos(2pi/3)+C
C=0
значит будет иметь вид F(x)=-2cos2x
2) log(10)(3x-1)-log(10)(x)<log(10)(0.6)
log(10)(3x-1/x)<log(10)(0.6)
3x-1/x<0.6
3x-1<0.6x
2.4x<1
x<1/2.4
3) Найдем высоту самой грани так как угол 30гр по теореме синусов x=8/sin30=16
теперь проекция 16^2-8^2=8V3
и сторону так как в два раза больше значит 16V3
теперь площадь основания будет равна S=256*3=768
V=1/3*768*8=2048
4) так как площадь боковой поверхности S=piRl=20
S=pir^2=4
r=2
L=10
H=10^2-2^2=4V6
V=1/3SH=1/3*4V6*4pi=16V6/3*pi
5)Опять же пирамида правильная четырехугольная , пирамида внутри пирамиды