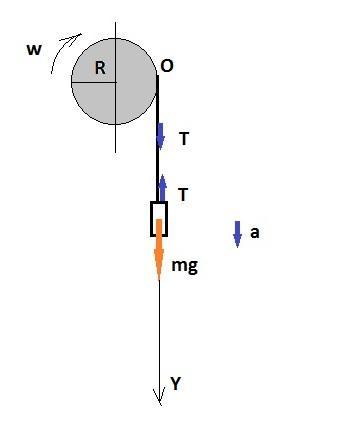
На однородный сплошной цилиндрический вал радиусом R = 50 см намотана легкая нить, к концу которой прикреплен груз массой m = 6,4 кг. Груз, разматывая нить, опускается с ускорением a=2 м/с . Определить момент инерции J вала и массу m1 вала.
Ответы
Ответ:
J = 6,25 кг·м²
m₁ = 50 кг
Объяснение:
Дано:
R = 50 см = 0,50 м
m = 6,4 кг
a = 2 м/с²
_______________
J - ?
m₁ - ?
1)
Сделаем чертеж. Ось OY направим вниз.
Составим уравнение для груза. По II закону Ньютона:
ma = mg - T
2)
Натяжение троса - это вес тела, движущегося с ускорением а вниз:
T = P = m·(g - a)
T = 6,4·(9,8-2) ≈ 50 Н
3)
Момент силы:
M = T·R = 50·0,50 = 25 Н·м
4)
Запишем уравнение вращательного движения для вала:
M = J·ε;
ε = a / R = 2 / 0,50 = 4 с⁻²
J = M / ε = 25 / 4 = 6,25 кг·м²
5)
Но момент инерции цилиндра:
J = m₁·R²/2
Тогда:
m₁ = 2·J / R² = 2·6,25 / 0,50² = 50 кг