Question

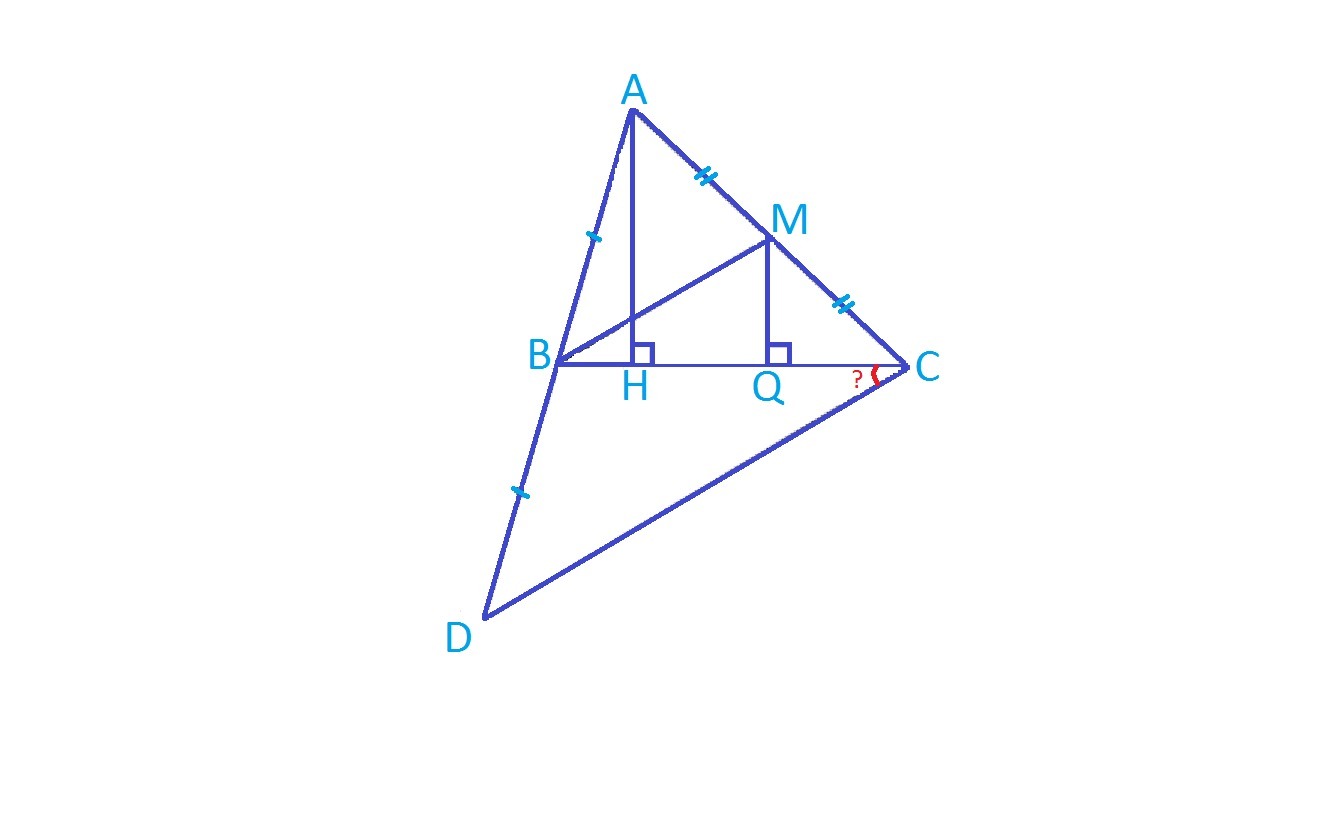
Высота AH остроугольного треугольника ABC равна его медиане BM. На продолжении стороны AB за точку B отложена точка D так, что BD=AB. Надите угол BCD.

Answer 1

Δ $ABC-$ остроугольный
$BM-$ медиана
$AH-$  высота
$BM=AH$
$AB$ ∩ $CD=D$
$AB=BD$
$textless BCD-$ ?

Δ $ABC-$ остроугольный
$AH$ ⊥ $BC$
$AM=MC$
$MQ$ ⊥ $BC$
$textless AHC= textless MQC=90к$
значит $AH$ ║ $MQ$
$MQ-$ средняя линия Δ $AHC$
$MQ= frac{1}{2} AH$
$AH=BM$ (по условию)
$MQ= frac{1}{2} BM$

Δ $BMQ-$ прямоугольный
$MQ= frac{1}{2} BM$  ⇒ $textless MBQ=30к$ ( катет, лежащий против угла в 30° равен половине гипотенузы)
$AB=BD$ (по условию)
$AM=MC$ (BM - медиана)
$BM-$ средняя линия Δ $ACD$
$BM$ ║ $DC$ 
$textless BCD= textless CBM=30к$ ( как накрест лежащие при параллельных прямых BM и CD и секущей BC)

Ответ: 30°