Question

Через вершину конуса проведена плоскость, пересекающая окружность основания по хорде, равной 6 корням из 3 и стягивающей дугу 120. Секущая плоскость составляет с плоскостью основания угол в 45 град. Найдите объем конуса.

 

Answer 1

Через вершину конуса проведена плоскость, пересекающая окружность основания по хорде, равной 6 корням из 3 и стягивающей дугу 120°.
Секущая плоскость составляет с плоскостью основания угол в 45°.
Найдите объем конуса.

 

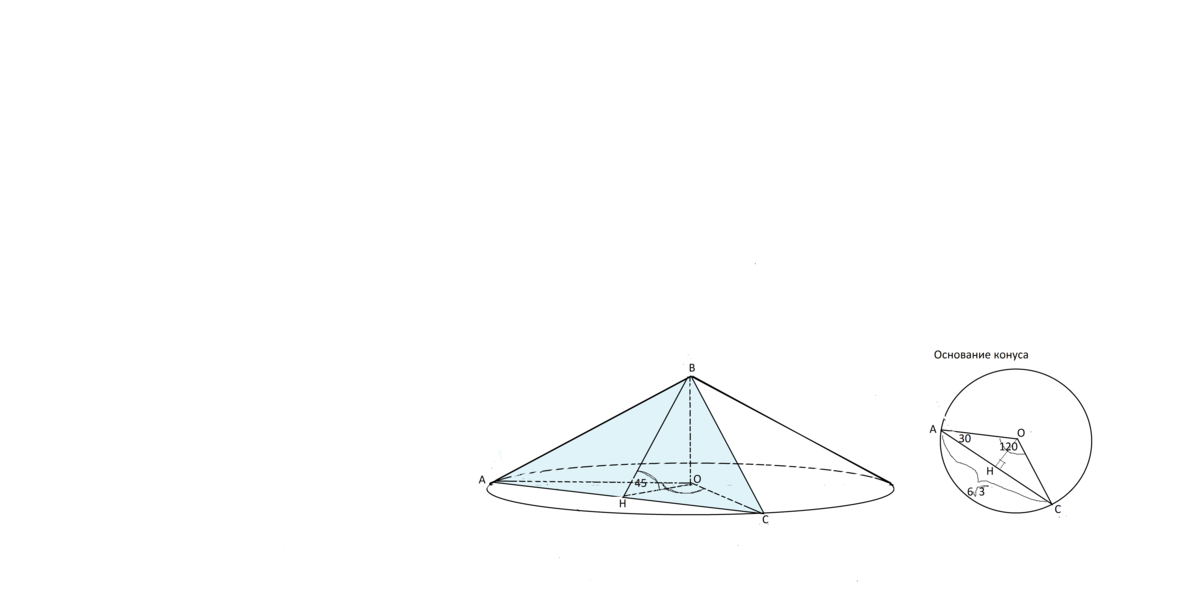
Рисунок дает представление о соотношении размеров конуса.
Отдельно сделаем рисунок основания конуса.
Рассмотрим его.
Треугольник АОС равнобедренный,

АС в нем - хорда - основание сечения АВС,
АО и ОС - проекции образующих, ограничивающих сечение, и равны радиусу основания;
ОН - расстояние от основания конуса до хорды.

Для решения нам нужно найти радиус ОА основания конуса и
ВО- его высоту.

Рассмотрим треугольник АОС.
Угол АОС =120°, углы ∠ОАС=∠ОСА=30°
∠AOH=60°
АН=АС:2=3√3
АО=r=AH:sin(60)={3√3}:{(√3):2}=6
ОН противолежит углу 30° и равен половине АО
ОН=6:2=3

Перейдем к основному рисунку.
По условию сечение образует с плоскостью основания ∠45°.
∠ВНО=45°⇒
∠НВО=45°
Треугольник НОВ - прямоугольный равнобедренный.
Отсюда ВО=ОН=3
Объем конуса равен 1/3 произведения площади основания на высоту:
V=Sh:3=36π*3:3=36π ( единиц объема)