окружность касается большего катета прямоугольного треугольника, проходит через его вершину противоположного острого угла, и ее центр лежит на гипотенузе. найдите радиус этой окружности, если катеты равны 4 и 3.
Ответы
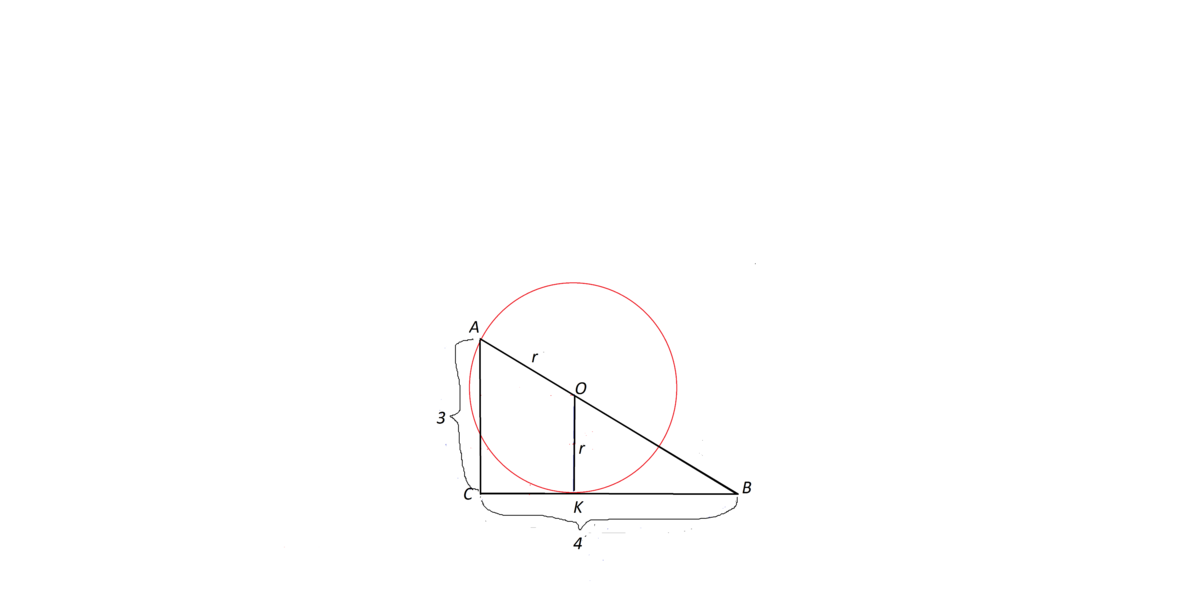
Cделаем рисунок, с ним гораздо легче следить за решением.
Обозначим вершины треугольника классическими А, В, С.
Из центра О опустим перпендикуляр на катет СВ.
Он соединяет центр окружности с точкой К касания с СВ и равен радиусу.
Отрезок гипотенузы АО также равен радиусу окружности.
Рассмотрим треугольники АВС и ВОК.
Они подобны: оба прямоугольные и имеют общий острый угол.
Поэтому справедливо отношение:
АС:ОК=АВ:ОВ
ОВ=АВ-r
Найдем АВ - гипотенузу треугольника АВС.
Это египетский треугольник, и, поскольку АС =3, СВ=4, АВ будет равна 5. ( можно проверить по т. Пифагора),
АС:ОК=АВ:ОВ
3:r=5:(5-r)
5r=15-2r
8 r=15
r=1,875