Предмет: Геометрия,
автор: feelingtime
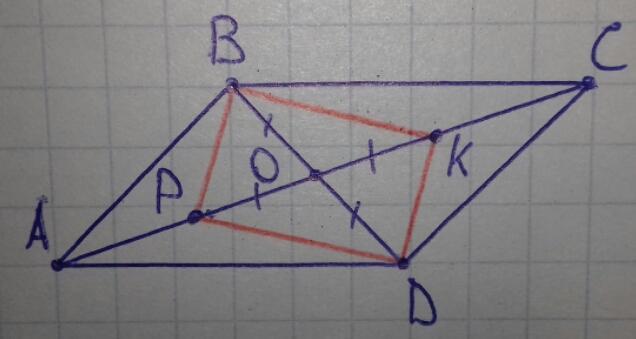
в параллелограмме abcd с острым углом А диагонали пересекаются в точке О, на отрезках АО и ОС взяты точки P и K соответственно.OP = OD OK=OB доказать что PBKD прямоугольник
Ответы
Автор ответа:
0
В параллелограмме диагонали делятся точкой пересечения пополам, поэтому BO=OD.
По условию: BO=OK и DO=OP.
В итоге KO=BO=DO=PO, поэтому KO+OP=BO+OD; KP=BD.
В четырёхугольнике PBKD диагонали делятся точкой пересечения пополам (PO=OK и BO=OD), значит, PBKD - параллелограмм. Ещё диагонали KP и BD равны, поэтому PBKD - прямоугольник, что и требовалось доказать.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: ogggoo
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: dimastepanenko097
Предмет: Математика,
автор: Sone4kasone4ka